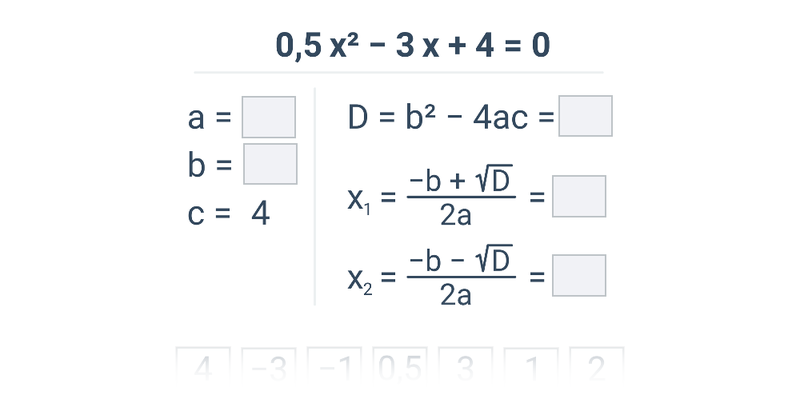Diskriminant (latinsky discriminare – rozlišit) je hodnota získaná z koeficientů polynomu, která umožňuje určit vlastnosti jeho kořenů, aniž bychom je znali. Používá se při řešení algebraických rovnic, především kvadratických, a také při studiu vlastností polynomických funkcí.Je-li diskriminant nulový, rovnice má přesně jeden kořen. Je-li však hodnota diskriminantu záporná, rovnice žádné řešení (v oboru reálných čísel) nemá.Podle hodnoty D určíme počet a hodnotu případných kořenů rovnice: Pro D < 0 pak kvadratická rovnice nemá reálné kořeny. Pro D = 0 pak kvadratická rovnice má jeden reálný kořen . Tento kořen se také někdy nazývá dvojnásobný kořen.
Jak poznat kvadratickou rovnici : Kvadratickou rovnicí s neznámou x rozumíme rovnici, kterou lze ekvivalentními úpravami převést na tvar ax2+bx+c=0,a,b,c∈R,a≠0. Výrazy ax2, bx, c se nazývají kvadratický člen, lineární člen, absolutní člen kvadratické rovnice. O počtu kořenů rovnice ax2+bx+c=0, kde a≠0, v oboru reálných čísel, resp.
Co když vyjde diskriminant 0
Když je diskriminant kladný má kvadratická rovnice dvě řešení, když je disriminant roven nule, má kvadratická rovnice jedno řešení. Když vyjde diskriminant záporný, kvadratická rovnice nemá v oboru reálných čísel řešení.
Jak odvodit diskriminant : Diskriminant polynomu je výraz, který můžeme vyjádřit pomocí kořenů polynomu (diskriminant n neurčitých) nebo pomocí koeficientů daného polynomu (homogenní polynom vzhledem k těmto koeficientům). Jeho hodnota vypovídá o povaze kořenů polynomu.
Obecnou kvadratickou rovnici řešíme pomocí diskriminantu. Když je diskriminant kladný má kvadratická rovnice dvě řešení, když je disriminant roven nule, má kvadratická rovnice jedno řešení. Když vyjde diskriminant záporný, kvadratická rovnice nemá v oboru reálných čísel řešení.
Soustava lineárních rovnic má nekonečně mnoho řešení tehdy, když grafy jednotlivých rovnic tvoří tu samou přímku.
Co kdyz vyjde rovnice 0 0
0 0 = – platná rovnost ⇒3 je řešením rovnice, Z nabízených čísel jsou řešením rovnice čísla 1 a 3.Řešíme-li lineární rovnici ax + b = 0, kde a, b ∈ R , nastane právě jedna z možností: a) a = 0 , rovnice má jedno řešení x = − b a ; b) a = 0, b = 0 , řešením rovnice jsou všechna x ∈ R ; c) a = 0, b = 0 , rovnice nemá řešení.Soustava lineárních rovnic nemá žádné řešení tehdy, když jsou grafy jednotlivých rovnic navzájem rovnoběžné. Nekonečně mnoho řešení. Soustava lineárních rovnic má nekonečně mnoho řešení tehdy, když grafy jednotlivých rovnic tvoří tu samou přímku.
Soustava nemá žádné řešení – po dosazení se ve vzniklé rovnici odečte i druhá neznámá a vznikne neplatná rovnost. Soustava má nekonečně mnoho řešení – po dosazení se ve vzniklé rovnici odečte i druhá neznámá a vznikne platná rovnost.
Co kdyz rovnice vyjde 0 0 : 0 0 = – platná rovnost ⇒3 je řešením rovnice, Z nabízených čísel jsou řešením rovnice čísla 1 a 3.
Jak řešit rovnici : Rovnici upravujeme pomocí ekvivaletních úprav: přičítání a odčítání stejného výrazu k oběma stranám rovnice, úpravy výrazů na levé a pravé straně. Pomocí takových úprav ji převedeme do tvaru x = a x = a x=a, kde a je řešení. Od obou stran rovnice odečteme 2 x 2x 2x.
Co je to kvadratický Trojčlen
Předpoklady: 020501, 020503, 020508, 020509 Kvadratický trojčlen je každý trojčlen, který je možné zapsat ve tvaru 2 ax bx c + + , kde 0 a ≠ . konkrétní čísla za x. Ptáme se: „Kdy se trojčlen rovná nule “ kvadratická rovnice.
Soustava nemá žádné řešení – po dosazení se ve vzniklé rovnici odečte i druhá neznámá a vznikne neplatná rovnost. Soustava má nekonečně mnoho řešení – po dosazení se ve vzniklé rovnici odečte i druhá neznámá a vznikne platná rovnost.Pro řešení rovnice v součinovém tvaru využijeme pravidlo, že součin dvou a více činitelů je roven nule právě tehdy, když alespoň jeden z činitelů je nula. Každý činitel položíme roven nule.
Co znamená 0x : 0x je protokol, který umožňuje výměnu aktiv založených na platformě Ethereum peer-to-peer (P2P). Protokol vyvinutý společností 0x Labs slouží jako otevřený standard a základní stavební prvek DeFi pro všechny vývojáře, kteří vyžadují možnosti výměny.