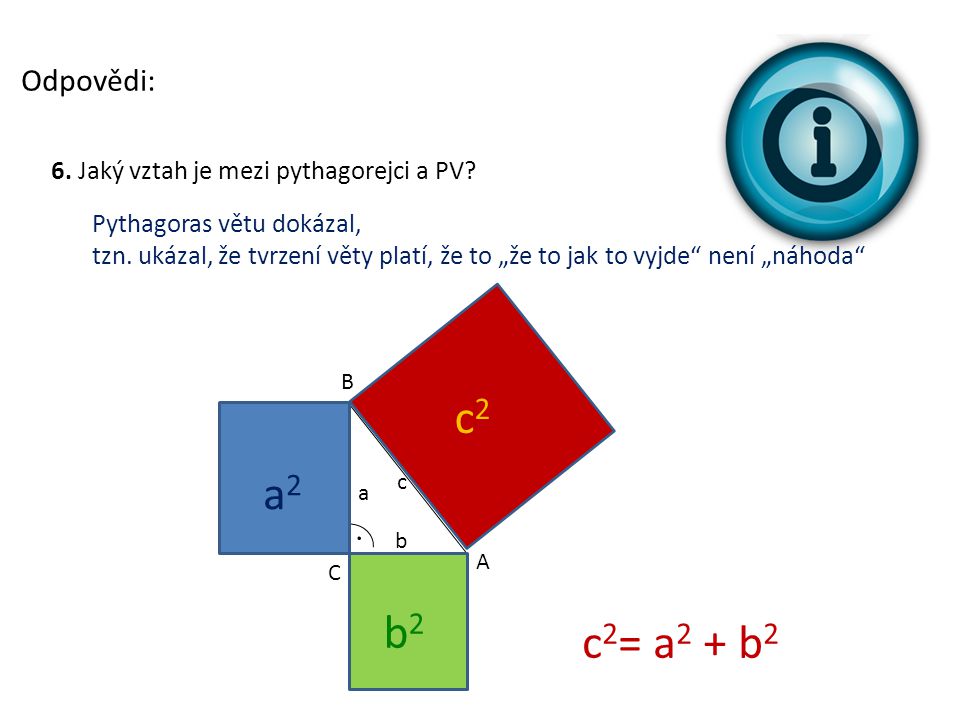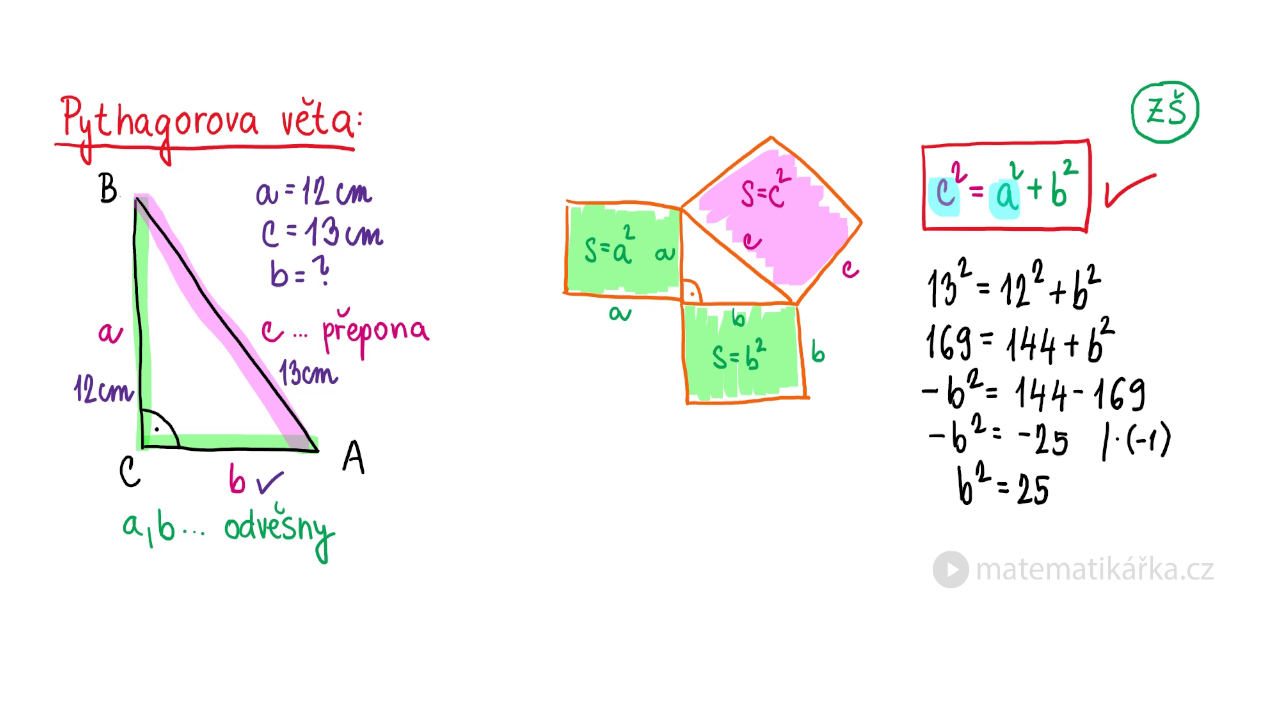
Pythagorova věta popisuje vztah, který platí mezi délkami stran pravoúhlých trojúhelníků v euklidovské rovině. Umožňuje dopočítat délku třetí strany takového trojúhelníku, pokud jsou známy délky dvou zbývajících stran.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.
Jak se pocita přepona trojúhelníku : Vzorce: Pythagorovu větu můžeme zapsat vztahem c² = a² + b², kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.
Co rekl Pythagoras
Pythagorás ze Samu
První Řek, který si uvědomil, že Večerka i Jitřenka jsou jedna a tatáž planeta – Venuše. Prohlásil, že Země je kulatá a rozšířil Anaximandrův model sfér. V matematice proslul Pythagorovou větou pro pravoúhlý trojúhelník (kvadrát velikosti přepony je roven součtu kvadrátů velikostí odvěsen).
Co plati v pravoúhlém trojúhelníku : V pravoúhlém trojúhelníku platí, že velikost plochy čtverce nad odvěsnou je stejná jako plocha obdélníku (vztyčeného výškou) ve čtverci nad odvěsnou. Pythagorova věta: V každém pravoúhlém trojúhelníku je součet obsahů čtverců nad odvěsnami stejný jako obsah čtverce nad přeponou.
Pythagorova věta popisuje vztah, který platí mezi délkami stran pravoúhlého trojúhelníku. Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami.

Přepona pravoúhlého trojúhelníku je vždy ta strana, která se nachází naproti pravému úhlu. Tato strana je v trojúhelníku nejdelší. Další dvě strany jsou nazvány protilehlá a přilehlá odvěsna. Jsou takto nazvány vzhledem k danému úhlu.
Kdy zemřel Pythagoras
Metapontum Village, ItáliePythagoras / ÚmrtíPythagoras ze Sámu (přesněji Pýthagorás, řec. Πυθαγόρας ο Σάμιος, okolo 570 př. n. l. ostrov Samos – po 510 př. n. l. Krotón v jižní Itálii) byl řecký filozof, matematik, astronom i kněz.Pravoúhlý trojúhelník je takový trojúhelník, jehož jeden vnitřní úhel je pravý, tzn. má velikost 90°; jinými slovy, dvě ze stran pravoúhlého trojúhelníka jsou na sebe kolmé.
Každý trojúhelník má tři výšky. Menší straně odpovídá větší výška. Přímky, na nichž leží výšky, se protínají v jednom bodě, který se nazývá ortocentrum nebo také výšiště. Ortocentrum leží uvnitř trojúhelníku, pokud je ostroúhlý.
Jak poznat protilehlou a přilehlou : V pravoúhlém trojúhelníku je přepona nejdelší stranou. "Protilehlá odvěsna" je strana naproti zadanému úhlu a "přilehlá odvěsna" je strana vedle daného úhlu.
Co to je Odvěsna a přepona : Nejdelší strana v pravoúhlém trojúhelníku se nazývá přepona. Přepona leží proti pravému úhlu. Zbývající dvě strany nazýváme odvěsny. Odvěsny svírají pravý úhel.
Co vymyslel Pythagoras
V tomto ohledu Pythagoras první použil matematiku ve službách fyziky! Do obecného povědomí vešla především tzv. Pythagorova věta o „součtech čtverců“ stran v pravoúhlém trojúhelníku. Ono c2 = a2 + b2 zná bez nadsázky téměř každý.
François Viète (1540–1603) představil použití písmen v rovnicích a položil tak základ moderní matematické notaci. Matematika byla vždy důležitým nástrojem přírodních věd a pokroky v matematice se téměř vždy shodovaly s vývojem v jiných předmětech, v neposlední řadě ve fyzice a astronomii.Pravoúhlý trojúhelník má jeden vnitřní úhel o velikosti 90 stupňů. Oba zbývající vnitřní úhly musí mít nutně velikost menší než 90 stupňů, aby součet vnitřních úhlů byl roven 180 stupňů. Součet dvou zbývajících úhlů je tedy právě 90 stupňů.
Jak poznat síň cos TG : Goniometrické funkce a pravoúhlý trojúhelník
- Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony.
- Kosinus ( cos) úhlu α je poměr délky odvěsny přilehlé úhlu α a délky přepony.
- Tangens ( tan) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky odvěsny přilehlé úhlu α.