Dvě přímky p(P, u) a q(Q, v) jsou totožné právě tehdy, jsou-li rovnoběžné a leží-li bod Q na přímce p. Jsou-li přímky p(P, u) a q(Q, v) totožné, pak jsou rovnoběžné (u je násobkem v) a bod Q leží na přímce p.Věta sss: Dva trojúhelníky, které se shodují ve všech třech stranách, jsou shodné.Střed úsečky můžeme dále určovat odhadem pomocí kružítka: Sestrojíme oblouky dvou shodných kružnic se středy v krajních bodech úsečky AB a poloměrem přibližně poloviny úsečky AB. Střed úsečky pak snadno odhadneme jako střed úsečky, jejíž krajní body jsou průsečíky obou oblouků s úsečkou AB.
Jak se značí shodnost trojúhelníků : sss, sus, uu Označení věty zkratkou vyjadřuje, kterými údaji trojúhelníky porovnáváme. VĚTA sss Každé dva trojúhelníky, které mají sobě rovné poměry délek všech tří dvojic odpovídajících si stran, jsou podobné.
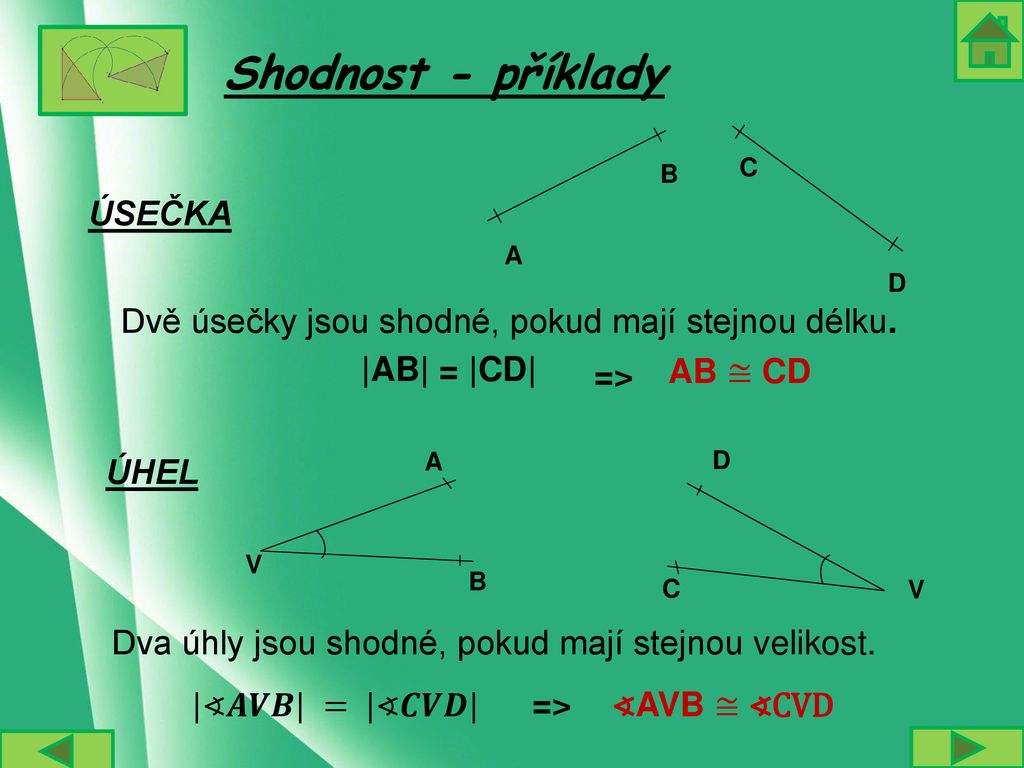
Kdy jsou dvě úsečky shodné
Dvě úsečky jsou shodné, když mají stejnou délku. Př.
Jak zjistit obecnou rovnici : Obecná rovnice. Obecná rovnice přímky v rovině má tvar ax+by+c=0 , kde a,b,c jsou nějaká reálná čísla taková, že alespoň jedno z čísel a a b není rovno 0. Body ležící na této přímce jsou právě ty bodyX=(x,y), jejichž souřadnice splňují uvedenou rovnost.
Jestliže se dva trojúhelníky shodují ve dvou vnitřních úhlech, pak jsou podobné. Jestliže dva trojúhelníky mají stejný poměr délek dvou párů odpovídajících si stran a shodují se v úhlu jimi sevřeném, pak jsou podobné.
Jestliže dva rovinné útvary můžeme přemístit tak, že se kryjí,budeme je nazývat shodnými útvary. Jestliže se dva trojúhelníky shodují ve všech třech stranách, pak jsou shodné.
Kdy jsou úsečky shodné
Shodné úsečky mají stejnou délku.Způsobů je několik, ale nejklasičtější je protnutí dvou kružnic se stejným poloměrem, větším než je polovina úsečky, a se středy na koncích úsečky. Spojnice těchto průsečíků je k přímce kolmá a půlí ji (prochází středem).Dva úhly jsou shodné, když mají stejnou velikost (je to jediná charakteristika úhlu).
- Věta „sss“ Shodují-li se dva trojúhelníky ve všech třech odpovídajících si stranách, pak jsou shodné.
- Věta „sus“ Shodují-li se dva trojúhelníky ve dvou stranách a úhlu jimi sevřeném, jsou shodné.
- Věta „usu“ Shodují-li se dva trojúhelníky v jedné straně a v obou úhlech k ní přilehlých, jsou shodné.
- Věta „Ssu“
Co patří do shodných zobrazení : Shodná zobrazení Zobrazení f v rovině je shodné zobrazení, jestliže pro každé dva body X, Y roviny a jejich obrazy X', Y' platí |XY|=|X'Y'|. Shodné zobrazení v rovině se rovněž nazývá shodnost.
Co znamená shodnost v geometrii : Shodné zobrazení je v geometrii takové zobrazení mezi Euklidovskými prostory, které zachovává vzdálenost. Shodné zobrazení prostoru do sebe se nazývá shodnost. V elementární školské geometrii se studují shodnosti v rovině a (trojrozměrném) prostoru.
Jak zjistit zda bod leží na přímce
Body A, B, C leží na jedné přímce, právě tehdy, když je vektor AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC. AB = (1; -2; 2), AC = (-1; 2; -1).
Obecná rovnice přímky v rovině má tvar: a x + b y + c = 0 ax+by+c=0 ax+by+c=0, kde konstanty a a b jsou souřadnice normálového vektoru a c reálné číslo.Definice: Zobrazení v rovině se nazývá podobným zobrazením (podobností), jestliže každé úsečce AB přiřazuje úsečku A´B´ pro jejíž velikost platí . Koeficient k nazýváme poměr podobnosti.
Jaký úhel svírá trojúhelník : Věta sus — v trojúhelníku jsou dány délky dvou stran a velikost úhlu, který svírají (menší než 180°).