
Goniometrické funkce
| α | cotg α | |
|---|---|---|
| 1. kvadrant | 0–90° | + |
| 2. kvadrant | 90–180° | − |
| 3. kvadrant | 180–270° | + |
| 4. kvadrant | 270–360° | − |
Goniometrické funkce a pravoúhlý trojúhelník
- Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony.
- Kosinus ( cos) úhlu α je poměr délky odvěsny přilehlé úhlu α a délky přepony.
- Tangens ( tan) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky odvěsny přilehlé úhlu α.
Tangens
| úhel | 0° | 180° |
|---|---|---|
| sinus úhlu | 0 | 0 |
| cosinus úhlu | 1 | -1 |
| tangens úhlu | 0 | 0 |
Jak se pocita tg : Existují ještě dvě další goniometrické funkce, tangens a kotangens. Hlavní rozdíl oproti předchozím goniometrickým funkcím je ten, že tangens a kotangens pracuje pouze s odvěsnami, nepracuje s přeponou. Tangens úhlu α se rovná poměru délky protilehlé odvěsny ku délce přilehlé odvěsny.
Kolik je cos 2pí
| X [º] | X [rad] | cos(2x) |
|---|---|---|
| 1 | 0,0175 | 0,9994 |
| 2 | 0,0349 | 0,9976 |
| 3 | 0,0524 | 0,9945 |
| 4 | 0,0698 | 0,9903 |
Jak poznat kvadrant : Kartézské souřadnice
Vodorovná osa se v kartézských souřadnicích obvykle označuje jako osa x a míří doprava, svislá osa jako osa y a míří vzhůru. Kvadranty se pak číslují od kladné poloosy x proti směru otáčení hodinových ručiček jako „první“ až „čtvrtý“, resp. jako I, II, III, IV nebo 1, 2, 3, 4.
Tangens úhlu alfa se rovná poměru délky protilehlé odvěsny ku délce přilehlé odvěsny v pravoúhlém trojúhelníku. Tangens obvykle značíme buď tg nebo tan.
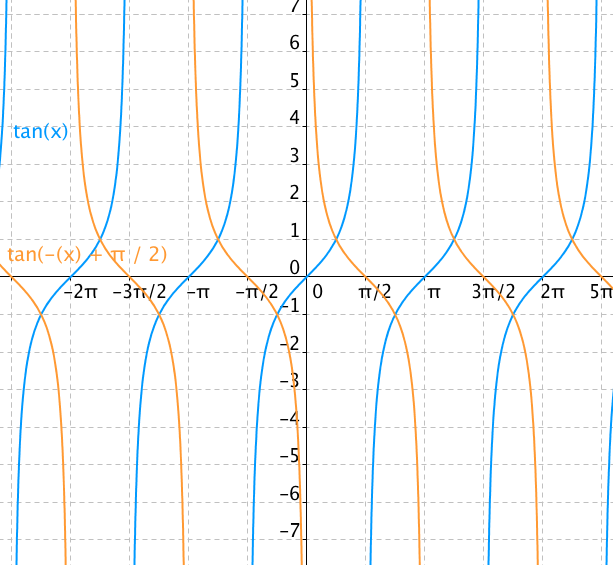
Nyní se budeme zabývat dalšími dvěma goniometrickými funkcemi tangens (značka tg) a kotangens (značka cotg).
Kolik je síň 45
Hodnoty sinus na jednotkové kružnici
| x (úhel) | ||
|---|---|---|
| 30° | π/6 | 1/12 |
| 150° | 5π/6 | 5/12 |
| 45° | π/4 | 1/8 |
| 135° | 3π/4 | 3/8 |
Tangens je goniometrická funkce. Je to funkce transcendentní, nelze ji obecně vyčíslit pomocí konečného počtu elementárních operací. Pro označení této funkce se obvykle používá značka tan (v českých publikacích běžně též tg) doplněná značkou nezávisle proměnné (zpravidla úhlu).Kolik je tangens 60 stupňů OK tangens je protilehlá ku přilehlé protilehlá k úhlu 60 stupňů je 2 odmocniny ze 3 2 druhé odmocniny ze 3 a přilehlá je 2. Přilehlá k úhlu 60 stupňů je 2.

Dosadíme do pravé strany, kde tangens třiceti stupňů je přibližně roven 0,5773 (viz kalkulačka na počítání hodnoty funkce tangens). | c | = 3 0,577 3 = 5,196. Pro tangens třicet stupňů existuje tabulková hodnota, platí, že:
Jak funguje kvadrant : kvadrant – úkoly jsou nedůležité, tedy jejich vykonáním se nepřiblížíme svým dlouhodobějším cílům nebo nekorespondují s životní vizí a směřováním, a zároveň nejsou naléhavé (nemají žádný nebo blížící se deadline). Sem patří aktivity jako surfování na sociálních sítích, koukání na nesmyslné pořady v TV, hraní her apod.
Co jsou kvadranty : Kvadrant (geometrie) – jedna ze čtyř částí roviny rozdělené dvěma navzájem kolmými přímkami, obdobně jedna ze čtyř částí prostoru rozděleného dvěma navzájem kolmými rovinami, též čtvrtina kruhu nebo obvodu kružnice. Kvadrant (geografie), též zemský kvadrant – čtvrtina zemského poledníku, tj. část mezi pólem a rovníkem.
Jaká je základní perioda funkce tangens
Odhad periody.
Většina lidí zná vlastně jen čtyři takové funkce, jmenovitě sinus a kosinus se základní periodou 2π a tangens a kotangens se základní periodou π.

Funkce tangens je definována v pravoúhlém trojúhelníku jako poměr protilehlé a přilehlé odvěsny. Jejím grafem je tangentoida. Funkce je definována v intervalu od 90 ° ± k · 180 ° do 270 ° ± k · 180 ° a nabývá hodnot od −∞ do +∞.Funkcí tangens je každému reálnému číslu u přiřazeno číslo yK . Důvod zobrazování hodnot funkce tangens na výše zmíněnou tečnu je zřejmý. Funkce tg x je poměr protilehlé odvěsny ku přilehlé. Velikost přilehlé odvěsny je 1, takže hodnota tg x je přímo yK .
Co to je síň : Sinus je goniometrická funkce nějakého úhlu. Zapisuje se jako sin θ, kde θ je velikost úhlu. Pro ostré úhly je definována v pravoúhlém trojúhelníku jako poměr protilehlé odvěsny a přepony (nejdelší strany). Definici lze konzistentně rozšířit jak na všechna reálná čísla, tak i do oboru komplexních čísel.



