
Hodnoty sinus na jednotkové kružnici
| x (úhel) | ||
|---|---|---|
| 165° | 11π/12 | 11/24 |
| 30° | π/6 | 1/12 |
| 150° | 5π/6 | 5/12 |
| 45° | π/4 | 1/8 |
Goniometrické funkce
| α | cotg α | |
|---|---|---|
| 1. kvadrant | 0–90° | + |
| 2. kvadrant | 90–180° | − |
| 3. kvadrant | 180–270° | + |
| 4. kvadrant | 270–360° | − |
Goniometrické funkce můžeme v pravoúhlém trojúhelníku vyjádřit následovně: Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony.
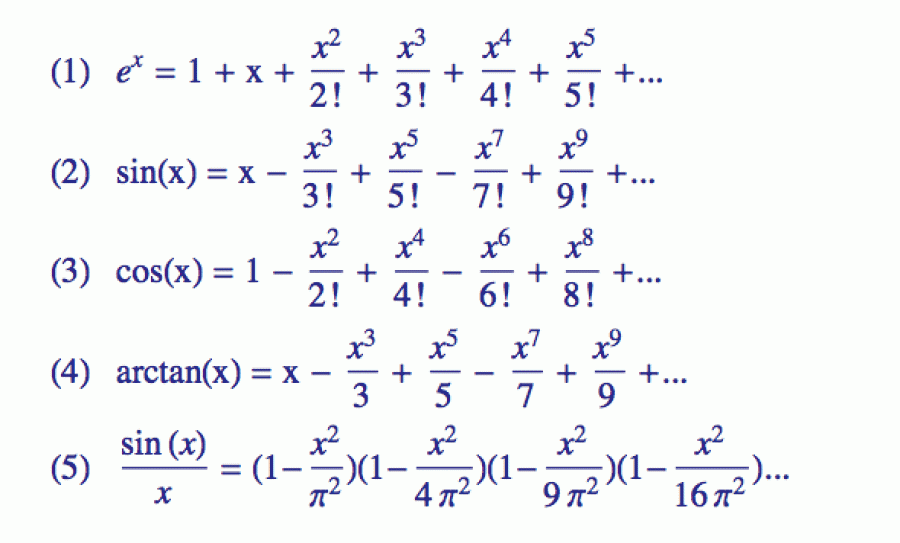
Kdy je sinus 0 : Nejprve definujeme sin(0) = 0, cos(0) = 1, sin(π/2) = 1, cos(π/2) = 0. Pro α z ⟨π/2,π⟩ definujeme sin(α) = sin(π − α) a cos(α) = −cos(π − α).
Kolik je sinus 90 stupňů
sin(90) = sin(2.035rad) = 0.8939.
Kolik je sinus 25 :
| X [º] | X [rad] | sin(x) |
|---|---|---|
| 23 | 0,4014 | 0,3907 |
| 24 | 0,4189 | 0,4067 |
| 25 | 0,4363 | 0,4226 |
| 26 | 0,4538 | 0,4384 |
Sinus je kladný ještě v kvadrantu druhém, tangens ve třetím a kosinus ve čtvrtém.
Před stiskem samotné klávesy sin, cos nebo tan, je třeba stisknout klávesu, která bývá označena symbolem INV, Shift, 2nd, nebo f–1. Inverzní funkce k sin bývá označována sin–1 nebo arcsin. Inverzní funkce ke cos se značí cos–1 nebo arccos. Inverzní funkce k tan se označuje tan–1 nebo arctan.
Jak poznat sinus a cosinus
Obě funkce jsou definovány na . Také to můžeme poznat z grafů obou funkcí, graf funkce sinus je souměrný podle počátku a graf funkce kosinus je souměrný podle osy . Obě jsou periodické, jejich nejmenší perioda je . Například je to vidět z grafů funkcí nebo z jednotkové kružnice.Přesněji „první“ maximum má v bodě x = π 2 a protože je to periodická funkce, tak má maximum také v každém bodě π 2 + 2 k π , kde k je celé číslo. Hodnota maxima je pak 1. Podobně pro minimum: sinus má minimum v bodech − π 2 + 2 k π , kde k je celé číslo a jeho hodnota je −1. Sinus je lichá a omezená funkce.sin(90) = sin(2.035rad) = 0.8939.
sin φ = Q/S je poměr mezi jalovým a zdánlivým výkonem, je to rovněž bezrozměrné číslo. tg φ = Q/P je poměr mezi jalovým a činným výkonem, je to rovněž bezrozměrné číslo.
Jak zadat do kalkulačky odmocniny : [SHIFT] [y√x] Tlačítko pro výpočet obecné odmocniny
Chcete-li vypočítat y-tou odmocninu z čísla x, stiskněte kombinaci tlačítek [x] [SHIFT] [y√x], zadejte číslo [y] a poté stiskněte tlačítko [=].
Kdy se používá sinus a kdy cosinus : V pravoúhlém trojuhelníku může sinus úhlu dosahovat hodnot mezi 0 až 1. Kosinus (cos): Kosinus úhlu v pravoúhlém trojúhelníku je definován jako poměr délky přilehlé strany k délce přepony trojúhelníka. V pravoúhlém trojuhelníku může kosinus úhlu dosahovat hodnot mezi 0 až 1.
Jak dát na Kalkulacce mocniny
Po výpočet mocnin kalkulačka nabízí speciální tlačítko (většinou x nebo yx), takže stačí jen zadat číslo, stisknout tlačítko pro mocninu a poté zadat číslo, které umocňujeme. Pro odmocniny kalkulačka většinou využívá tlačítko x√ a postup výpočtu je stejný jako u mocnin.
Když hledáme odmocninu třeba z 25, tak hledáme číslo, které po umocnění dá 25. To splňuje 5 ⋅ 5 5\cdot 5 5⋅5, ale také ( − 5 ) ⋅ ( − 5 ) (-5)\cdot (-5) (−5)⋅(−5). Odmocnina je však definována jako nezáporné číslo, takže 25 = 5 \sqrt{25} = 5 25 =5.Goniometrické funkce, jako jsou sinus, kosinus, tangens a cotangens, jsou základními nástroji pro popis vztahů mezi úhly a délkami stran v pravoúhlém trojúhelníku. Tyto funkce se používají k výpočtu poměrů mezi délkami stran trojúhelníka a příslušnými úhly.
Jak dát do kalkulačky odmocninu : [SHIFT] [y√x] Tlačítko pro výpočet obecné odmocniny
Chcete-li vypočítat y-tou odmocninu z čísla x, stiskněte kombinaci tlačítek [x] [SHIFT] [y√x], zadejte číslo [y] a poté stiskněte tlačítko [=].






