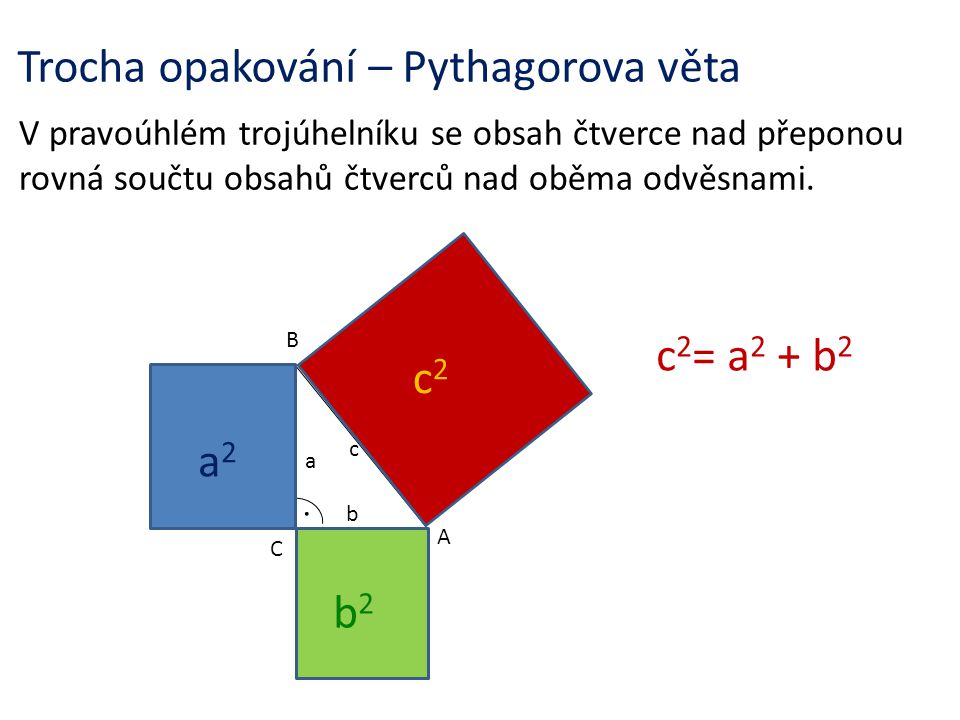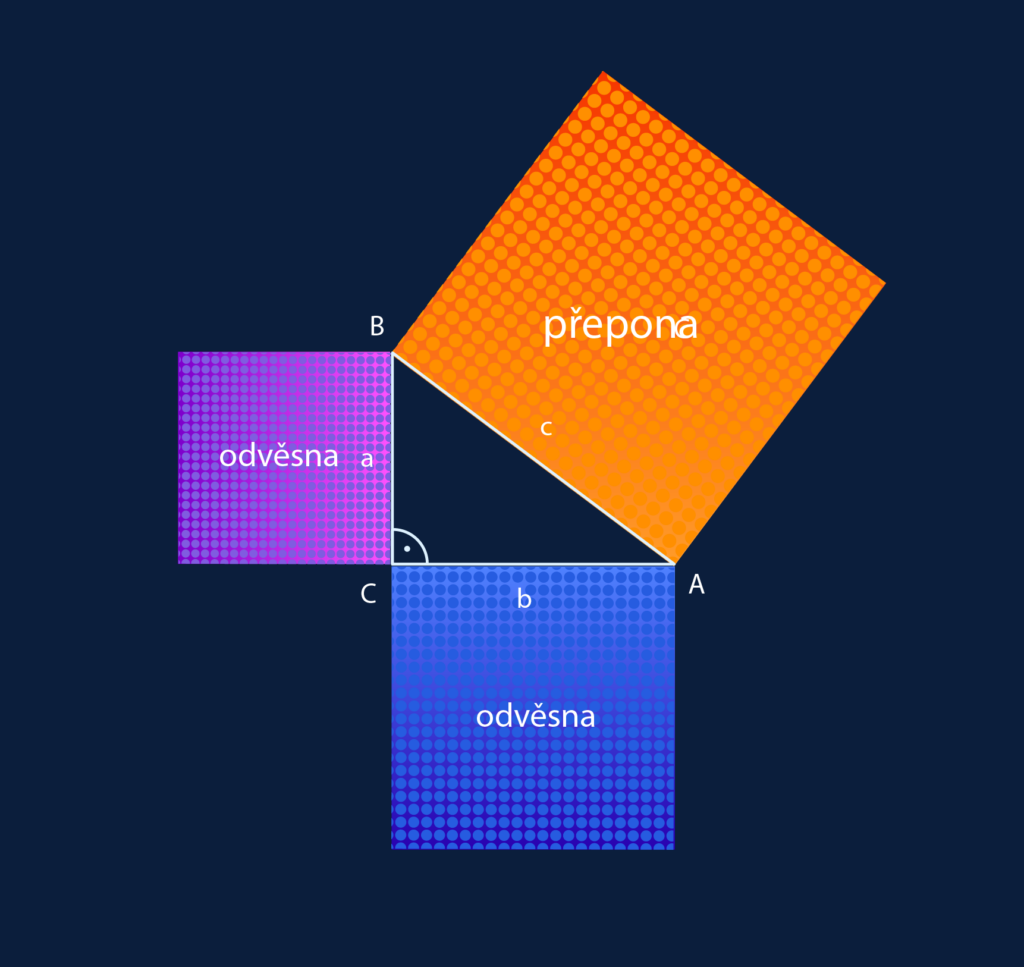
Pythagorova věta popisuje vztah, který platí mezi délkami stran pravoúhlých trojúhelníků v euklidovské rovině. Umožňuje dopočítat délku třetí strany takového trojúhelníku, pokud jsou známy délky dvou zbývajících stran.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .V pravoúhlém trojúhelníku platí, že velikost plochy čtverce nad odvěsnou je stejná jako plocha obdélníku (vztyčeného výškou) ve čtverci nad odvěsnou. Pythagorova věta: V každém pravoúhlém trojúhelníku je součet obsahů čtverců nad odvěsnami stejný jako obsah čtverce nad přeponou.
Kde jsou přepony a Odvesny : V pravoúhlém trojúhelníku je přepona nejdelší stranou. "Protilehlá odvěsna" je strana naproti zadanému úhlu a "přilehlá odvěsna" je strana vedle daného úhlu. Pro popsání stran pravoúhlého trojúhelníku používáme speciální terminologii.
Kdy plati Pythagorova věta
V každém pravoúhlém trojúhelníku platí , kde je délka přepony, , jsou délky jeho odvěsen.
Co rekl Pythagoras : Pythagorás ze Samu
První Řek, který si uvědomil, že Večerka i Jitřenka jsou jedna a tatáž planeta – Venuše. Prohlásil, že Země je kulatá a rozšířil Anaximandrův model sfér. V matematice proslul Pythagorovou větou pro pravoúhlý trojúhelník (kvadrát velikosti přepony je roven součtu kvadrátů velikostí odvěsen).
Pythagorova věta popisuje vztah, který platí mezi délkami stran pravoúhlého trojúhelníku. Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami.
Každý trojúhelník má tři výšky. Menší straně odpovídá větší výška. Přímky, na nichž leží výšky, se protínají v jednom bodě, který se nazývá ortocentrum nebo také výšiště. Ortocentrum leží uvnitř trojúhelníku, pokud je ostroúhlý.
Co platí v Rovnoramenném trojúhelníku
V rovnoramenném trojúhelníku jsou oba úhly u základny stejné. V pravoúhlém trojúhelníku je velikost jednoho úhlu 90°, součet velikostí zbývajících dvou úhlů je také 90°.Nejdelší strana v pravoúhlém trojúhelníku se nazývá přepona. Přepona leží proti pravému úhlu. Zbývající dvě strany nazýváme odvěsny. Odvěsny svírají pravý úhel.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
umime.to/FV2
Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami.
Kdy zemřel Pythagoras : Metapontum Village, ItáliePythagoras / Úmrtí
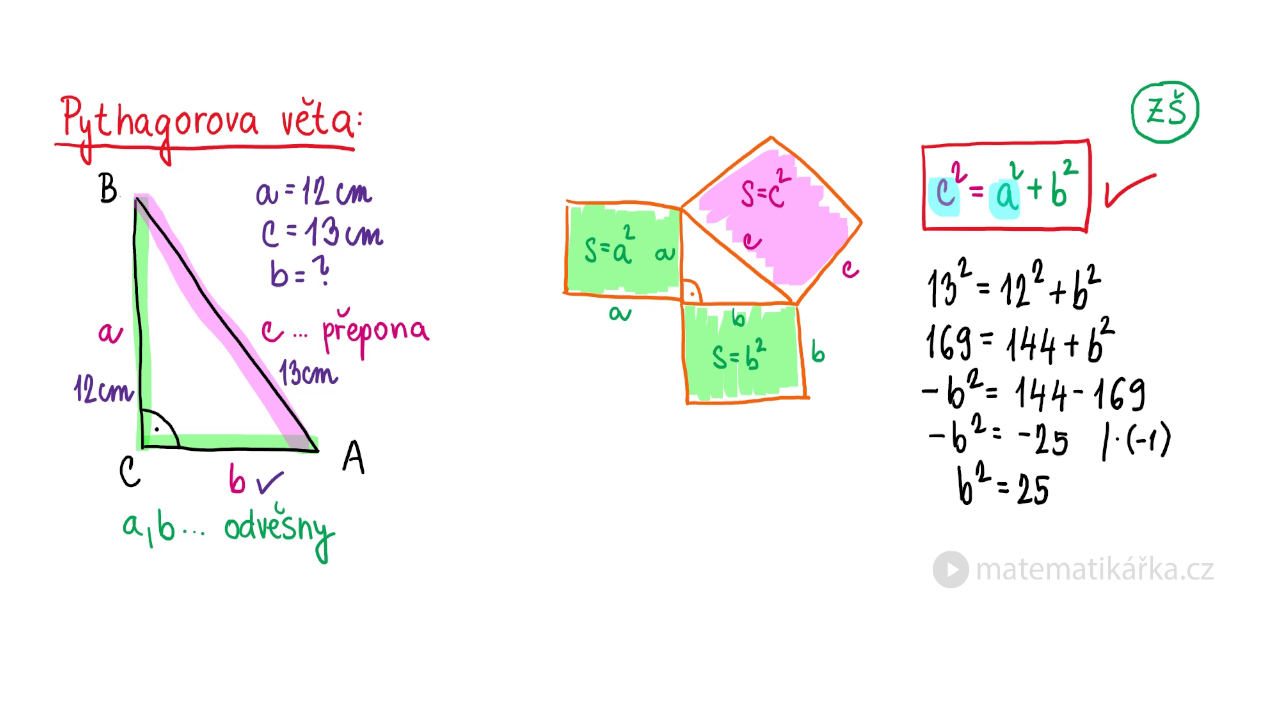
Jak se dělá Pythagorova věta : Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami. Pythagorovu větu můžeme zapsat vztahem c 2 = a 2 + b 2 c^2 = a^2 + b^2 c2=a2+b2, kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.
Co platí pro těžnice
Těžnice se protínají v jednom společném bodě, který označujeme T. Tento bod se nazývá těžiště a nachází se vždy uvnitř trojúhelníku. Těžiště rozděluje každou těžnici v poměru 2:1, kde větší část těžnice se nachází mezi vrcholem a těžištěm.
Těžiště se vždy nachází uvnitř trojúhelníku.
Těžiště představuje pomyslný střed trojúhelníku, pokud byste chtěli podržet trojúhelník na špičky tužky, pak byste měli tužku umístit právě pod těžiště, aby vám trojúhelník nespadl. Těžiště dále dělí délky těžnic v poměru 1:2.Rovnostranný trojúhelník je osově souměrný podle os každé ze tří stran ⇒ každá dvojice vnitřních úhlů je osově souměrná ⇒ každá dvojice vnitřních úhlů je shodná ⇒ všechny vnitřní úhly jsou shodné. Rovnostranný trojúhelník můžeme otočit o 120° a úhly přesune jeden na druhý ⇒ všechny vnitřní úhly jsou shodné.
Kde jsou odvěsny : Nejdelší strana v pravoúhlém trojúhelníku se nazývá přepona. Přepona leží proti pravému úhlu. Zbývající dvě strany nazýváme odvěsny. Odvěsny svírají pravý úhel.