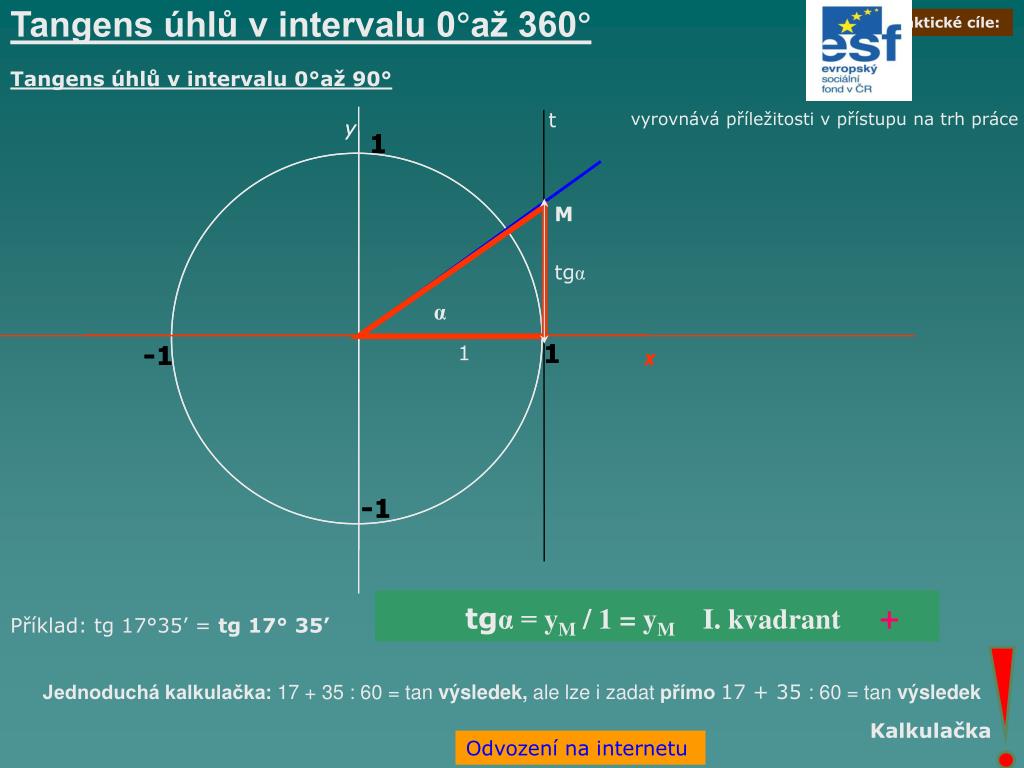
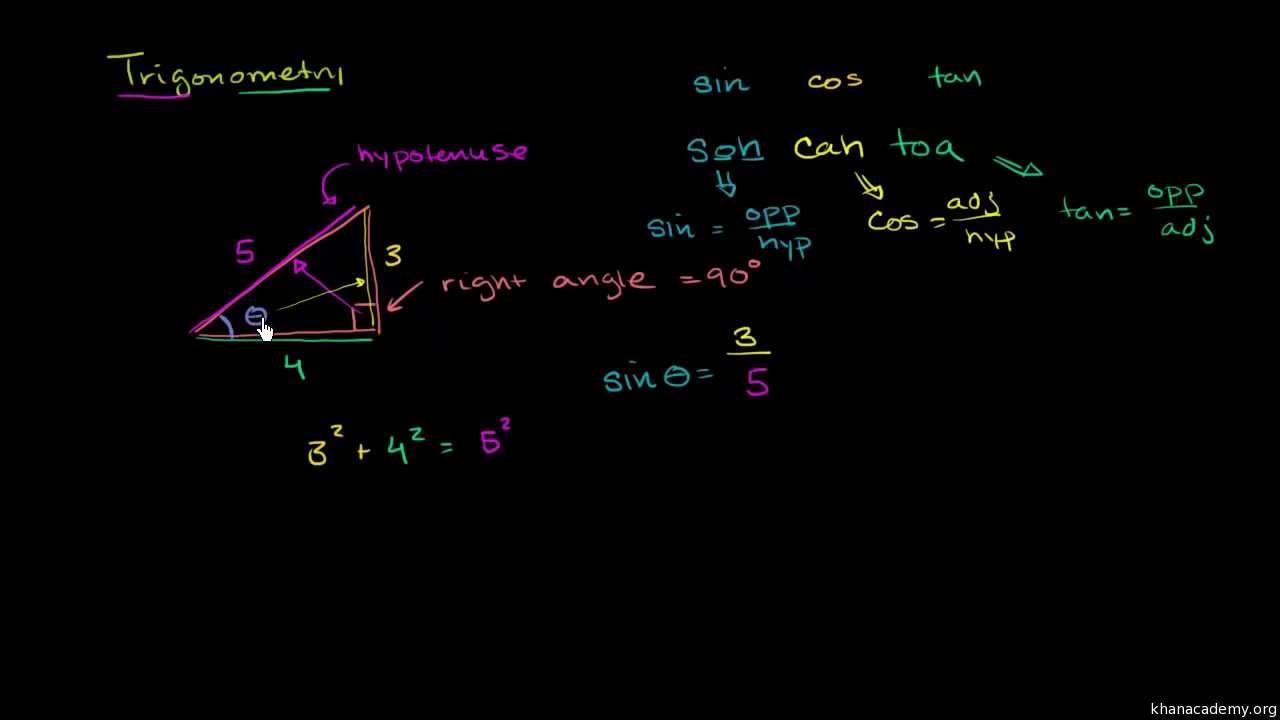Existují ještě dvě další goniometrické funkce, tangens a kotangens. Hlavní rozdíl oproti předchozím goniometrickým funkcím je ten, že tangens a kotangens pracuje pouze s odvěsnami, nepracuje s přeponou. Tangens úhlu α se rovná poměru délky protilehlé odvěsny ku délce přilehlé odvěsny.Tangens tak můžeme rozepsat jako podíl sinu a cosinu. Už bez odvození si povíme, že cotangens můžeme napsat jako obrácený zlomek, tj. podíl cosinus lomeno sinus.Tangens. Tangens úhlu alfa se rovná poměru délky protilehlé odvěsny ku délce přilehlé odvěsny v pravoúhlém trojúhelníku. Tangens obvykle značíme buď tg nebo tan.
Kdy je tg 0 : Tangens
| úhel | 0° | 180° |
|---|---|---|
| sinus úhlu | 0 | 0 |
| cosinus úhlu | 1 | -1 |
| tangens úhlu | 0 | 0 |
Jak vypočítat tangens na kalkulačce
Goniometrické funkce na kalkulačce
- Stiskneme příslušnou funkci – sin, cos, tg.
- Napíšeme hodnotu úhlu.
- Stiskneme tlačítko rovná se.
- Výsledek je zapsán buď v podobě zlomku, případně v podobě desetinného čísla.
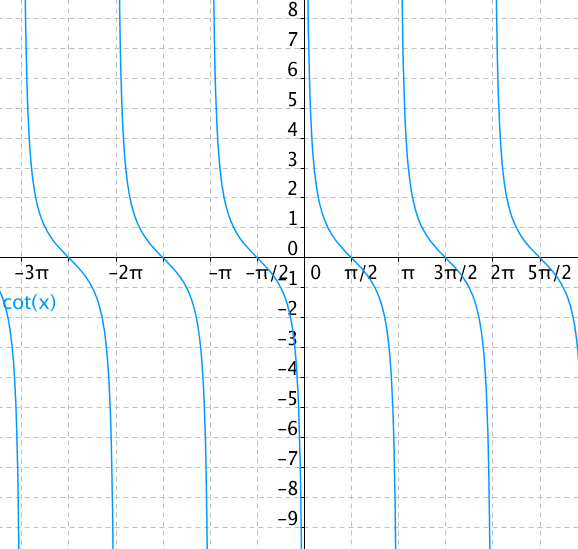
Kolik je tangens : Funkce tangens je definována v pravoúhlém trojúhelníku jako poměr protilehlé a přilehlé odvěsny. Jejím grafem je tangentoida. Funkce je definována v intervalu od 90 ° ± k · 180 ° do 270 ° ± k · 180 ° a nabývá hodnot od −∞ do +∞.
Tangens je goniometrická funkce. Je to funkce transcendentní, nelze ji obecně vyčíslit pomocí konečného počtu elementárních operací. Pro označení této funkce se obvykle používá značka tan (v českých publikacích běžně též tg) doplněná značkou nezávisle proměnné (zpravidla úhlu).
Sinus a kvadranty
| Stupně | Radiány | sin (x) |
|---|---|---|
| 0° | 0 | 0 |
| 90° | π/2 | 1 |
| 180° | π | 0 |
| 270° | 3π/2 | −1 |
Jaká je základní perioda funkce tangens
Odhad periody.
Většina lidí zná vlastně jen čtyři takové funkce, jmenovitě sinus a kosinus se základní periodou 2π a tangens a kotangens se základní periodou π.Kolik je tangens 60 stupňů OK tangens je protilehlá ku přilehlé protilehlá k úhlu 60 stupňů je 2 odmocniny ze 3 2 druhé odmocniny ze 3 a přilehlá je 2. Přilehlá k úhlu 60 stupňů je 2.Tangens ( tan) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky odvěsny přilehlé úhlu α.
Goniometrické funkce
| α | cotg α | |
|---|---|---|
| 1. kvadrant | 0–90° | + |
| 2. kvadrant | 90–180° | − |
| 3. kvadrant | 180–270° | + |
| 4. kvadrant | 270–360° | − |
Kolik stupňů je tangens : Funkce tangens je definována v pravoúhlém trojúhelníku jako poměr protilehlé a přilehlé odvěsny. Jejím grafem je tangentoida. Funkce je definována v intervalu od 90 ° ± k · 180 ° do 270 ° ± k · 180 ° a nabývá hodnot od −∞ do +∞.
Kolik je tangens 2 :
| X [º] | X [rad] | tg(x) |
|---|---|---|
| 1 | 0,0175 | 0,0175 |
| 2 | 0,0349 | 0,0349 |
| 3 | 0,0524 | 0,0524 |
| 4 | 0,0698 | 0,0699 |
Jak určit periodická funkce
Periodickou funkci poznáme z grafu funkce. Jestliže je celý graf určen jen částí, která se neustále opakuje, pak je to graf periodické funkce. Funkce f je periodická, právě když existuje takové reálné číslo T > 0 ,že pro funkci f platí: Pro všechna x z definičního oboru leží v definičním oboru i x+T a zároveň
Dosadíme do pravé strany, kde tangens třiceti stupňů je přibližně roven 0,5773 (viz kalkulačka na počítání hodnoty funkce tangens). | c | = 3 0,577 3 = 5,196. Pro tangens třicet stupňů existuje tabulková hodnota, platí, že: V prvním kvadrantu mají funkce sinus, kosinus i tangens (kotangens) kladnou hodnotu.
Kolik je síň 180 : Sinus a kvadranty
| Stupně | Radiány | sin (x) |
|---|---|---|
| 0° | 0 | 0 |
| 90° | π/2 | 1 |
| 180° | π | 0 |
| 270° | 3π/2 | −1 |