Body A, B, C leží na jedné přímce, právě tehdy, když je vektor AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC.Jak poznáme, o jakou se jedná kuželosečku Většinou se to dá rozpoznat už na začátku i před úpravami. Podíváme se na členy x a y. Pokud bude v rovnici jenom x nebo y na druhou a to druhé x a nebo y bude pouze na prvou, tak to zřejmě bude parabola.Jak určit body ležící na přímce je jednoduché – stačí zvolit jednu jeho souřadnici a z obecné rovnice dopočítat druhou. Zvolme si například hodnotu x-ové souřadnice jako 1. Dosadíme do obecné rovnice přímky a dopočítáme y-ovou souřadnici 2⋅1 – y + 3 = 0, y = 5.
Jak zjistit zda jsou vektory rovnoběžné : Dva vektory a, b jsou rovnoběžné právě tehdy, když jeden z nich je násobkem druhého, tj. když existuje takové reálné číslo k, že platí a = kb .
Jak se značí bod na přímce
Bod – je základní geometrický pojem, bod obvykle označujeme křížkem a značíme jej velkým písmenem. Your browser does not support this audio format. Přímka – se zadává dvěma body, neboť každými dvěma body lze vést právě jednu přímku. Značíme ji dvěma body nebo častěji malým písmenem.
Jak se počítá odchylka přímek : Odchylka přímky a roviny
Je-li přímka p kolmá k rovině ρ, je jejich vzájemná odchylka φ = π/2. Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ. Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q.
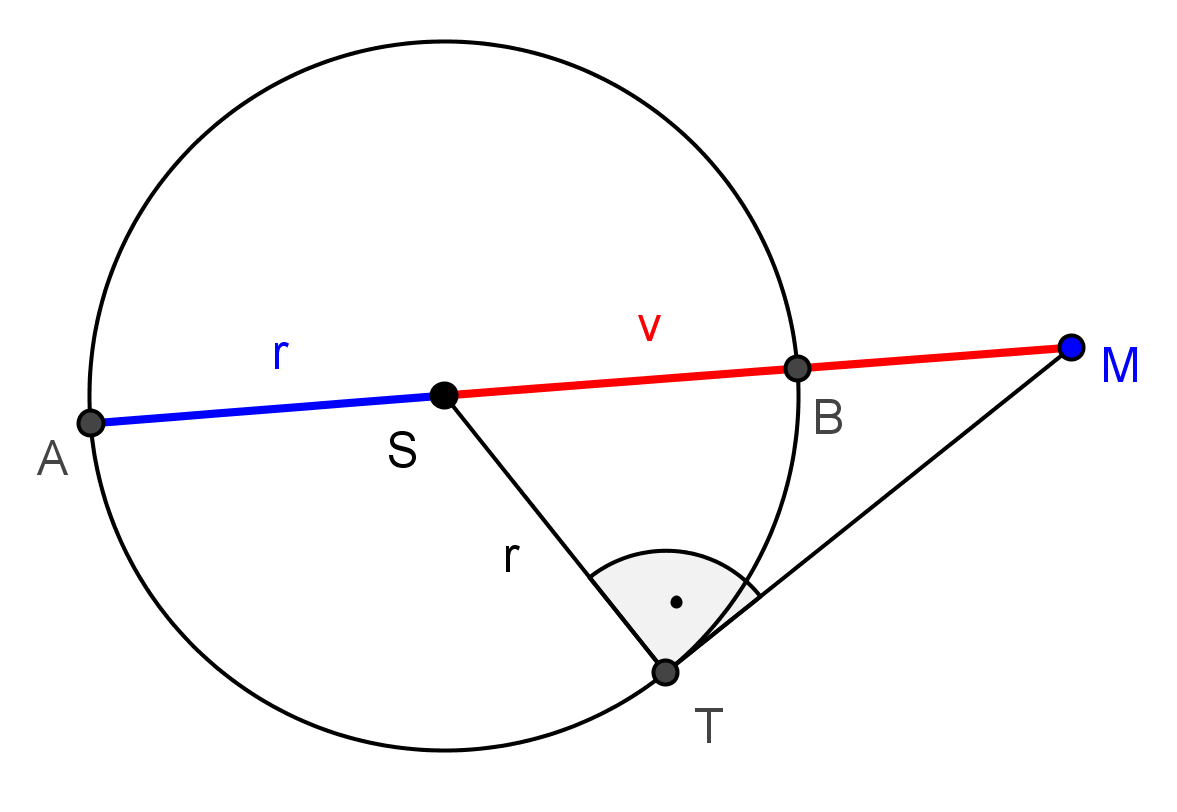
V euklidovské geometrii je kružnice množina všech bodů v rovině, které leží ve stejné vzdálenosti, označované jako poloměr, od pevně daného bodu, zvaného střed. Kružnice jsou jednoduché uzavřené křivky, rozdělující rovinu na vnitřek a vnějšek.
SEČNA KRUŽNICE je přímka, která má s kružnicí společné právě dva různé body.
Jak vypočítat střed kružnice
S kompasem nakreslete oblouk ze středu kruhu do bodu "A" a také oblouk do bodu "B". Pomocí pravítka přenesete střed kompasu na jeden z těchto bodů. Nakreslete další oblouk z bodu "A" až kde se protíná s obloukem z bodu "B". Místo protínání oblouků je střed kruhu.Jednotlivé orientované úsečky, které reprezentují (představují) vektor u, nazýváme umístění vektoru u. Souřadnice vektoru určujeme jako rozdíl souřadnic konečného a počátečního bodu. u = AB = B – A.Obecná rovnice přímky v rovině má tvar ax+by+c=0 , kde a,b,c jsou nějaká reálná čísla taková, že alespoň jedno z čísel a a b není rovno 0. Body ležící na této přímce jsou právě ty bodyX=(x,y), jejichž souřadnice splňují uvedenou rovnost.
Graficky se bod znázorňuje křížkem, malým kolečkem nebo kroužkem, označuje se velkým tiskacím písmenem.
Jak se vyznačuje bod : Bod – je základní geometrický pojem, bod obvykle označujeme křížkem a značíme jej velkým písmenem. Your browser does not support this audio format. Přímka – se zadává dvěma body, neboť každými dvěma body lze vést právě jednu přímku. Značíme ji dvěma body nebo častěji malým písmenem.
Jak vypočítat prumernou odchylku : Průměrná odchylka je součet absolutních hodnot rozdílu každého datového bodu a průměru datové sady, dělený počtem prvků v datové sadě.
Co to je odchylka přímek
Odchylka dvou různoběžných přímek je velikost každého z ostrých nebo pravých úhlů, které spolu přímky svírají. Odchylka dvou rovnoběžných přímek je 0°. Př. 1: Srovnej planimetrickou definici odchylky dvou přímek se stavem ve stereometrii a navrhni její stereometrickou definici.
Kruh se značí velkým písmenem a je dán středem a poloměrem, zapisuje se K(S;r), kde K- je název kruhu, takže když se bude jmenovat M, bude tam místo písmene K písmeno M.Kružnice vepsaná
- sestrojíme libovolné kružnice u všech tří vrcholů
- v průsečíku se stranami sestrojíme vždy dvojici stejných kružnic.
- spojnicí průsečíků kružnic z bodu 2 je osa úhlu.
- v průsečíku os leží střed kružnice vepsané
- ze středu sestrojíme kolmici na libovolnou stranu trojúhelníka.
Co je to Thaletova věta : Thaletova věta je matematická věta o velikosti úhlů trojúhelníků vytvořených nad průměrem kružnice. Je pojmenována po Thalétovi z Milétu, který ji jako první dokázal. Kružnice, která je součástí konstrukce Thaletovy věty, bývá označována jako Thaletova kružnice.