Strana, která není shodná s rameny, se nazývá základna. Vrchol naproti základně se nazývá hlavní vrchol.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .Pro výpočet obsahu trojúhelníku použijeme vzorec obsah = (strana krá výška)/2.
Jak najít těžiště v trojúhelníku : Těžiště se vždy nachází uvnitř trojúhelníku.
Těžiště představuje pomyslný střed trojúhelníku, pokud byste chtěli podržet trojúhelník na špičky tužky, pak byste měli tužku umístit právě pod těžiště, aby vám trojúhelník nespadl. Těžiště dále dělí délky těžnic v poměru 1:2.
Jak zjistit jednu stranu trojúhelníku
Trojúhelníky hrají v geometrii klíčovou roli, protože mnoho problémů lze řešit tak, že složitější obrazce rozdělíme na trojúhelníky a následně pracujeme s nimi. Značení stran a úhlů v trojúhelníku: Proti vrcholu A je strana a, proti vrcholu B je strana b a proti vrcholu C je strana c.
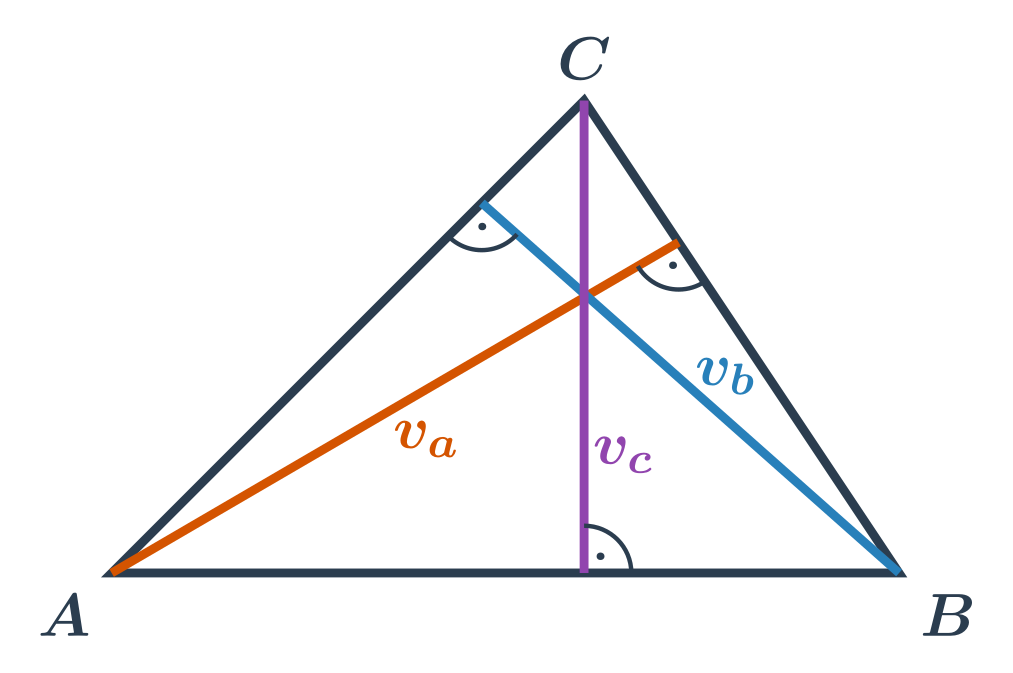
Co je to výška v trojúhelníku : Výška trojúhelníku je vzdálenost vrcholu trojúhelníku od protější strany. Je to úsečka, jejíž jeden krajní bod je vrchol a je kolmá na protější stranu k tomuto vrcholu. Každý trojúhelník má tři výšky.
Goniometrické funkce a pravoúhlý trojúhelník
- Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony.
- Kosinus ( cos) úhlu α je poměr délky odvěsny přilehlé úhlu α a délky přepony.
- Tangens ( tan) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky odvěsny přilehlé úhlu α.
Pythagorova věta: základní použití
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Jak se určuje těžiště
Těžištěm homogenních geometricky symetrických těles je jejich geometrický střed. U nepravidelných těles zjistíme těžiště tak, že ho budeme zavěšovat v různých bodech, a kreslit si na ně svislice (těžnice). A těžiště se nachází v průsečíku těchto těžnic. Soustava pevně spojených těles má jedno společné těžiště.Střed můžete graficky vypočítat pomocí kružítka a pravítka. Například střed strany AB naleznete tak, že narýsujete dvě stejně velké kružnice se středem ve vrcholech A a B. Tyto kružnice musí mít poloměr větší než je polovina délky úsečky AB — ale tento poloměr musí být u obou kružnic stejný!V pravoúhlém trojúhelníku je přepona nejdelší stranou. "Protilehlá odvěsna" je strana naproti zadanému úhlu a "přilehlá odvěsna" je strana vedle daného úhlu.
Jak zjistit (bez rýsování), jestli je trojúhelník pravoúhlý Jestliže v trojúhelníku platí, že součet druhých mocnin délek dvou kratších stran je roven druhé mocnině délky nejdelší strany, potom je tento trojúhelník pravoúhlý.
Jak se značí výška : Výšky označujeme obvykle malým písmenem v s indexem názvu strany, ke které příslušná výška patří. Slovem výška označujeme v trojúhelníku jak úsečku, tak její délku. Konstrukce výšky trojúhelníku. Základem konstrukce výšky trojúhelníku je sestrojení kolmice k dané straně procházející protějším vrcholem.
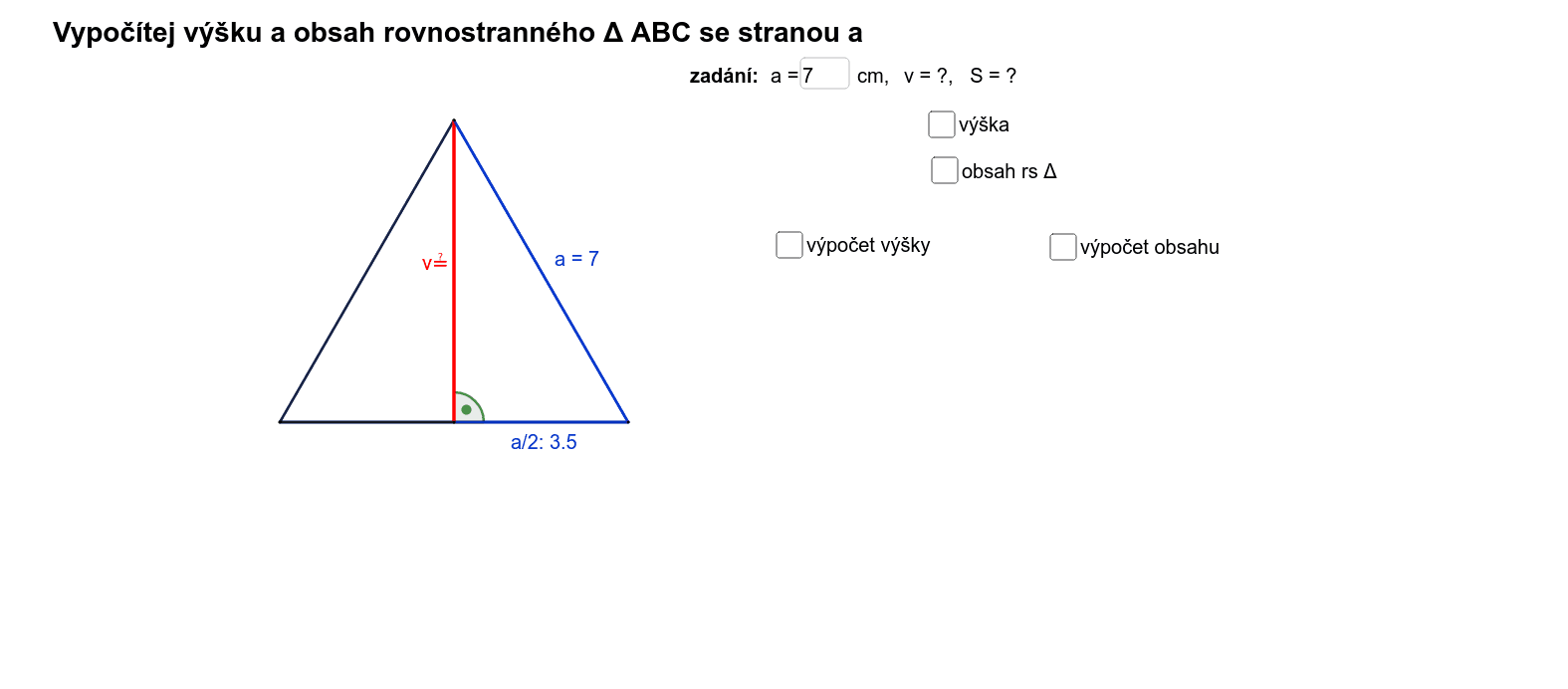
Jak se počítá výška trojúhelníku Pythagorova věta : Vypocitejte jeho vysku. Jak se pocita to cviceni To je pythagorova věta – c^2=a^2+b^2, kde c je rameno, a je výška a b polovina základny (výška v rovnoramenném trojúhelníku půlí základnu).
Kolik je cos 1
| X [º] | X [rad] | cos(x) |
|---|---|---|
| 1 | 0,0175 | 0,9998 |
| 2 | 0,0349 | 0,9994 |
| 3 | 0,0524 | 0,9986 |
| 4 | 0,0698 | 0,9976 |
Nejprve definujeme sin(0) = 0, cos(0) = 1, sin(π/2) = 1, cos(π/2) = 0.Nejdelší strana v pravoúhlém trojúhelníku se nazývá přepona. Přepona leží proti pravému úhlu. Zbývající dvě strany nazýváme odvěsny.
Jak poznat pravoúhlý trojúhelník podle délky stran : Jak zjistit (bez rýsování), jestli je trojúhelník pravoúhlý Jestliže v trojúhelníku platí, že součet druhých mocnin délek dvou kratších stran je roven druhé mocnině délky nejdelší strany, potom je tento trojúhelník pravoúhlý.