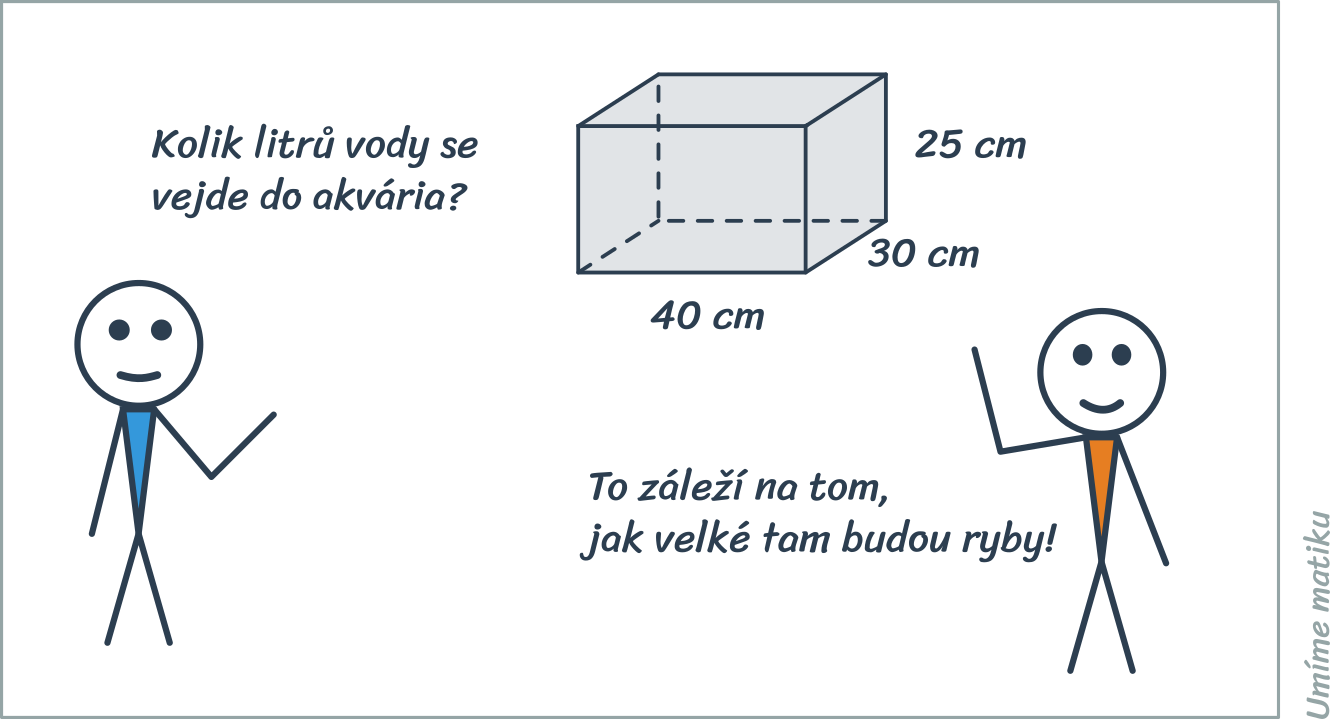
Vzorec pro výpočet objemu místnosti je tedy: V = a * b * c, kde a je délka, b je šířka a c je výška místnosti. Například, pokud má místnost délku 5 metrů, šířku 4 metry a výšku 3 metry, objem místnosti bude V = 5 * 4 * 3 = 60 metrů krychlových.Objem/obsah válce se spočítá jako plocha základny [S] × výška válce [v]. Plocha základny válce se spočítá z poloměru kružnice základny [r] jako: 3,14 (π) × r2. Celý vzorec pro výpočet objemu válce vypadá takto: [V] = π × r2 × v.Vzorce pro objem „hranatých“ těles vychází z obsahu podstavy a výšky tělesa. Objem libovolného hranolu je součin obsahu podstavy a výšky: V = S p ⋅ v V=S_p\cdot v V=Sp⋅v.
Jak Vypocitat objem Kulateho bazenu : Co je výpočet kubíku
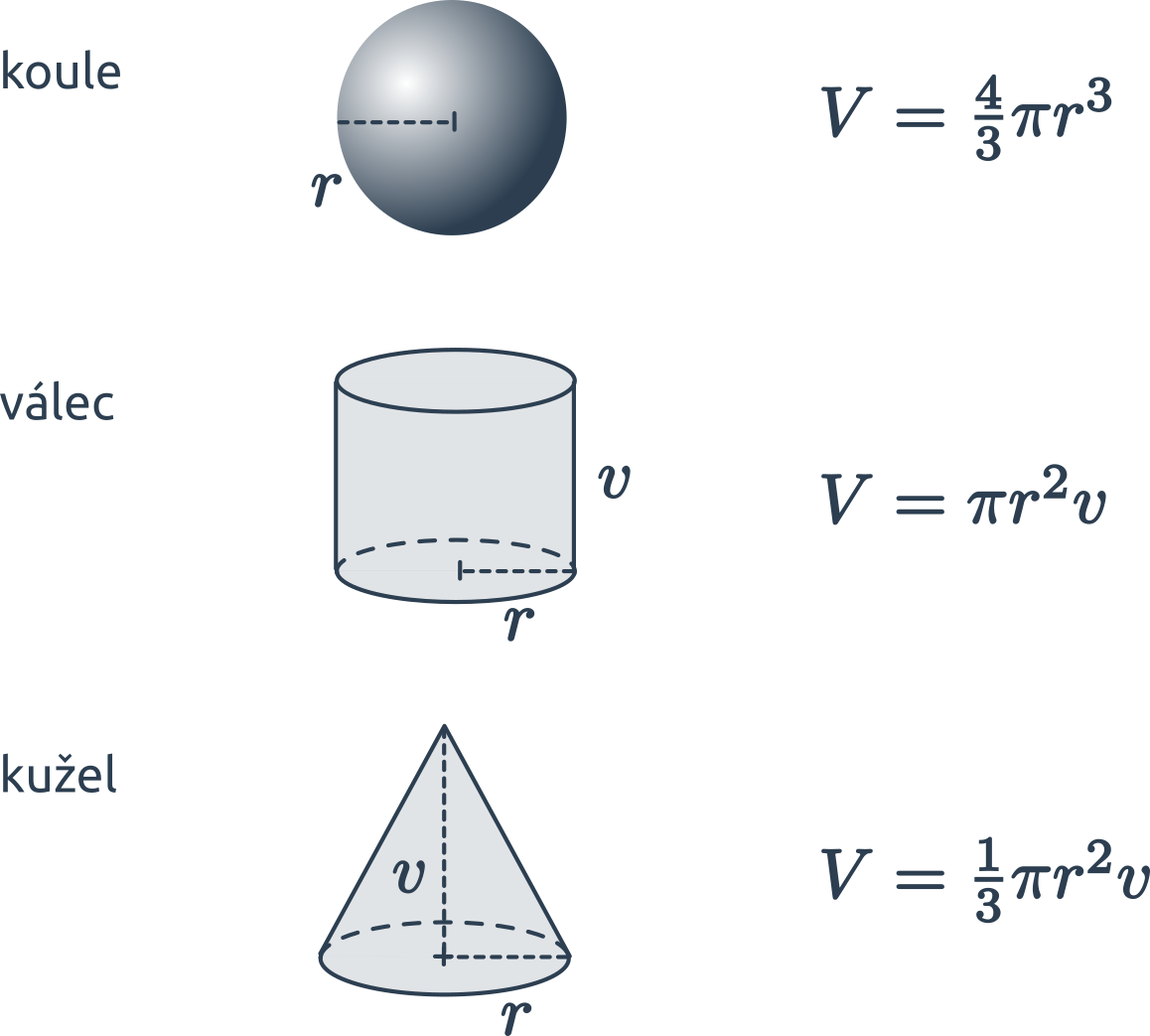
- Kruhový bazén: V=π*r2*v (r – poloměr, v – výška) 1 litr vody = 1 dm3
- Obdélníkový bazén: V= a*b*c (rozměry výšky, šířky, hloubky)
- Obdélníkový bazén se sestupným dnem: V = a*b*c+1/2*a*b*(c1-c2) (bazén se rozdělí na kvádr a hranol s trojúhelníkovou podstavou)
Jak vypočítat objem kvádru v litrech
Kvádr a krychle jsou speciální případy hranolu, jejich podstava je obdélník (čtverec) a výška je zbývající hrana. Objem kvádru je tedy součin délek jeho hran: V = a b c V = abc V=abc. Objem krychle vypočítáme stejným způsobem.
Jak se měří objem : K měření objemu kapalných těles používáme ODMĚRNÝ VÁLEC: ☞ Vybereme odměrný válec s vhodným měřicím rozsahem a stupnicí. ☞ Přelijeme do něj kapalinu, jejíž objem chceme měřit. ☞ Jakmile se hladina kapaliny ve válci ustálí, přečteme údaj na jeho stupnici → Díváme se přitom v rovině hladiny.
Změříme si vnitřní rozměry a vypočítáme podle známého vzorce objemu kvádru V = a*b*c. Při naměřené délce 150 cm, šířce 45 cm a hloubce 30 cm počítáme 150*45*30 = 202 500 cm³ = 202 l = 0,2 kubíků. U atypických rozměrů vany bude náš výpočet více nepřesný.

K měření objemu kapalných těles používáme ODMĚRNÝ VÁLEC: ☞ Vybereme odměrný válec s vhodným měřicím rozsahem a stupnicí. ☞ Přelijeme do něj kapalinu, jejíž objem chceme měřit. ☞ Jakmile se hladina kapaliny ve válci ustálí, přečteme údaj na jeho stupnici → Díváme se přitom v rovině hladiny.
Jak spočítat m3 vody
Změříme si vnitřní rozměry a vypočítáme podle známého vzorce objemu kvádru V = a*b*c. Při naměřené délce 150 cm, šířce 45 cm a hloubce 30 cm počítáme 150*45*30 = 202 500 cm³ = 202 l = 0,2 kubíků.OBJEM hranolu vypočítáme jako součin obsahu podstavy (SP) a výšky hranolu (v). V = SP · v POVRCH hranolu je roven součtu obsahů obou podstav (SP) hranolu a obsahu pláště hranolu SPL (SPL = S1 + S2 + S3 + S4).Uměli byste určit objem nepravidelného tělesa, např. kamene Využijeme k tomu odměrný válec. Vybereme si vhodný odměrný válec, aby jím kámen volně prošel, aniž by se dotýkal stěn.
Obsah je mírou (tedy charakteristikou velikosti) dané dvourozměrné části prostoru. Základní jednotka: 1 m2. (metr čtvereční). Objem je veličina, která vyjadřuje velikost prostoru, kterou zabírá těleso.
Jak se pocitaji litry : NEJHLEDANĚJŠÍ PŘEVODY VELIČINY OBJEM
- 1 mililitr = 0,001 litrů 1 litr = 1 000 mililitrů
- 1 hektolitr = 100 litrů 1 krychlový metr = 1 000 litrů
- 1 litr = 0,01 hektolitrů 1 litr = 0,001 metrů krychlových.
- 1 decilitr = 100 mililitrů 1 decilitr = 0,1 litrů
- 1 litr = 10 decilitrů 1 mililitr = 1 x 10 -6 metrů krychlových.
Čím se dá změřit objem : Objem těles se měří odměrnými nádobami nebo odměrnými válci.
Co je to objem tělesa
Objem tělesa vyjadřuje kolik místa v prostoru těleso zaujímá. Můžeme si jej představit jako množství vody, které bychom potřebovali, kdybychom chtěli těleso „napustit“.
Metr krychlový (také metr kubický, hovorově často kubík) je jednotka objemu, značená m³, patřící do soustavy SI jako odvozená jednotka. Jeden metr krychlový je objem krychle s délkou hrany 1 metr. Rovná se objemu 1000 litrů.1) Nejefektivnější a nejpřesnější způsob určení objemu vodní soustavy je vypuštění vodní soustavy přes vodoměr a odečtení stavu vodoměru. Vodoměr měří objem kapaliny v m3, což odpovídá 1000 litrům kapaliny.
Jakou značku má objem : Objem se značí písmenem V (počáteční písmeno latinského slova volumen znamenající právě objem). Tedy objem V tělesa udává, jakou „část prostoru toto těleso zabírá“ ve srovnání s jednotkovou krychlí (krychle s hranou jednotkové délky).





