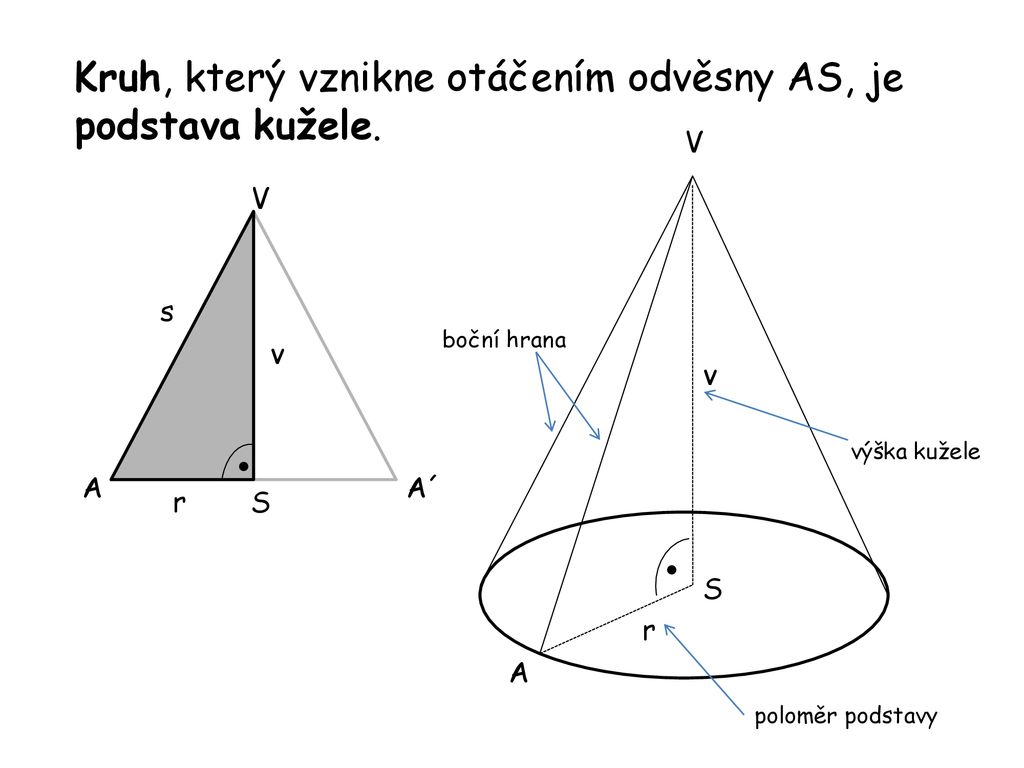
Kužel je geometrický útvar, který má podobu tělesa s jednou zakřivenou plochou a jedním vrcholem. Tato zakřivená plocha se nazývá plášť kužele, zatímco spodní plocha je kruh a vrchol je bodem, ze kterého vychází všechny generující úsečky (přímky spojující vrchol s body na obvodu kruhu).Kužel je prostorový geometrický útvar s kruhovou podstavou. Zužuje se směrem k jednomu bodu zvanému vrchol. Jde o útvar, který vznikne, když se kolem své osy otáčí rovnoramenný trojúhelník. Příkladem kuželu v běžném životě je kornout zmrzliny nebo dopravní kužel.Obsah pláště: S p l = 2 π r ⋅ v S_{pl}=2\pi r \cdot v Spl=2πr⋅v. Povrch válce: S = 2 π r ⋅ ( r + v ) S=2\pi r \cdot (r + v) S=2πr⋅(r+v)
Kolik má kužel hran : Geometrická tělesa
| Těleso | Kvádr | Kužel |
|---|---|---|
| Popis | Je to pravidelný čtyřboký hranol. Umí stát i ležet. | Rotuje okolo hrotu. |
| Základna | čtverec | kruh |
| Počet vrcholů | 8 | 1 |
| Počet hran | 12 | 1 |
Jak vypada Rotacni kužel
Kužel se od válce liší v tom, že má jen jednu podstavu a protilehlá strana tvoří špičku neboli vrchol. I kužel však může být kolmý nebo kosý, podstava může být různě klikatá, válcovitá nebo kulatá. Ve škole i v životě nejčastěji hovoříme o rotačním kuželu.
Jak narýsovat komolý kužel : Komolý kužel vznikne z kužele seříznutím špičky rovinou rovnoběžnou s rovinou podstavy. Objem takového tělesa určíme odečtením objemu odebíraného kužele od objemu původního, neseříznutého kužele. Podobně postupujeme i při určování obsahu pláště.
Jména zakončená na ‑l: typ kužel
jak podle tvrdého vzoru „hrad“, tak i podle měkkého vzoru „stroj“ (viz Skloňování mužských jmen kolísajících mezi měkkým a tvrdým skloňováním, Skloňování mužských jmen vzoru „hrad“ – 6.
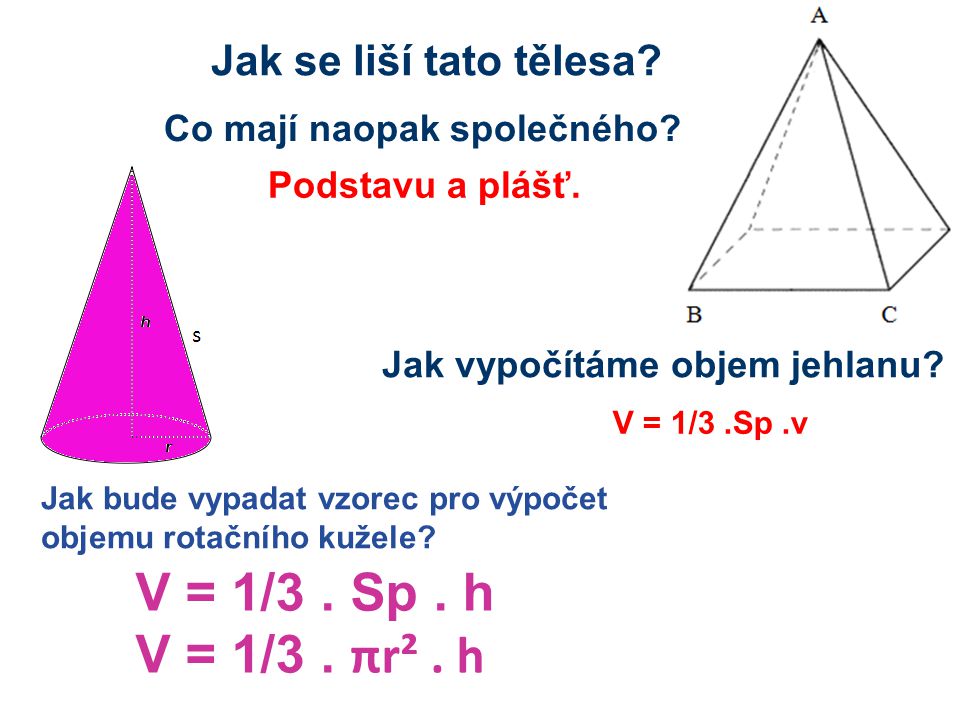
Objem kuželu vypočítáme jako součin 1/3 Π, druhé mocniny poloměru kruhu a délky výšky.
Jak se počítá objem kužele
Objem kužele je jedna třetina obsahu podstavy vynásobeného výškou, tedy V = 1 3 S p ⋅ v = 1 3 π r 2 v V = \frac13 S_p \cdot v = \frac13 \pi r^2 v V=31Sp⋅v=31πr2v.Kdybychom vzaly kužel s tímto množstvím vody, snadno bychom určili, kam rysku zakreslit (hladina vody v kuželu by nám jasně určila výšku). My ale dokážeme určit výšku kuželu, pokud známe jeho objem. Využijeme vztah ze vzorce V=π⋅r2⋅v⋅1/3.Rotační kužel vzniká otáčením pravoúhlého trojúhelníku okolo jedné z odvěsen. Povrch kužele vypočítáme jako součet plochy podstavy a plochy pláště.
umělecké dílo, z kt. jiné dílo vychází; předloha 2: studium literárních vzorů; snaha dostihnout klasické vzory (v umění) 5. celkový vzhled, tvar, forma něj.
Jaké jsou vzory mužského rodu : V češtině máme následující hlavní vzory:
- mužský rod. životný: pán, muž, soudce, předseda. neživotný: hrad, stroj.
- ženský rod: žena, růže, píseň, kost.
- střední rod: město, moře, kuře, stavení
Jak spočítat kubický metr : Například, pokud má místnost délku 5 metrů, šířku 4 metry a výšku 3 metry, objem místnosti bude V = 5 * 4 * 3 = 60 metrů krychlových.
Jak vypočítat výšku v kuželu
Kdybychom vzaly kužel s tímto množstvím vody, snadno bychom určili, kam rysku zakreslit (hladina vody v kuželu by nám jasně určila výšku). My ale dokážeme určit výšku kuželu, pokud známe jeho objem. Využijeme vztah ze vzorce V=π⋅r2⋅v⋅1/3.
Objem válce je π r² v a jeho plocha se dá zjistit pomocí vzorce 2 π r v + 2 π r². V tomto videu si tyto dva vzorce odvodíme. Tvůrce: Sal Khan.Vzorce pro výpočet
- Průměr: d = 2 × r.
- Poloměr: r = d / 2.
- Obvod podstavy: O = π d = 2 π r.
- Plocha podstavy kužele: P = π d2 / 4 = π r2
- Délka boční stěny: b = √ (r2 + h2)
- Plocha pláště kužele: Q = O × b / 2 = π r b.
- Celkový povrch/plocha kužele: S = P + Q = π r2 + π r b = π r (r + b)
Jak poznat vzor : Jak poznáme, který vzor použít
- Určíme rod podstatného jména.
- Podíváme se, zda jméno končí na souhlásku/samohlásku.
- Pokud končí např. na souhlásku, vybíráme ze vzorů, které končí také na souhlásku.
- Řekneme si jméno ve 2. pádě. Podle něj pak vybereme vzor, jehož 2. pád končí stejně.