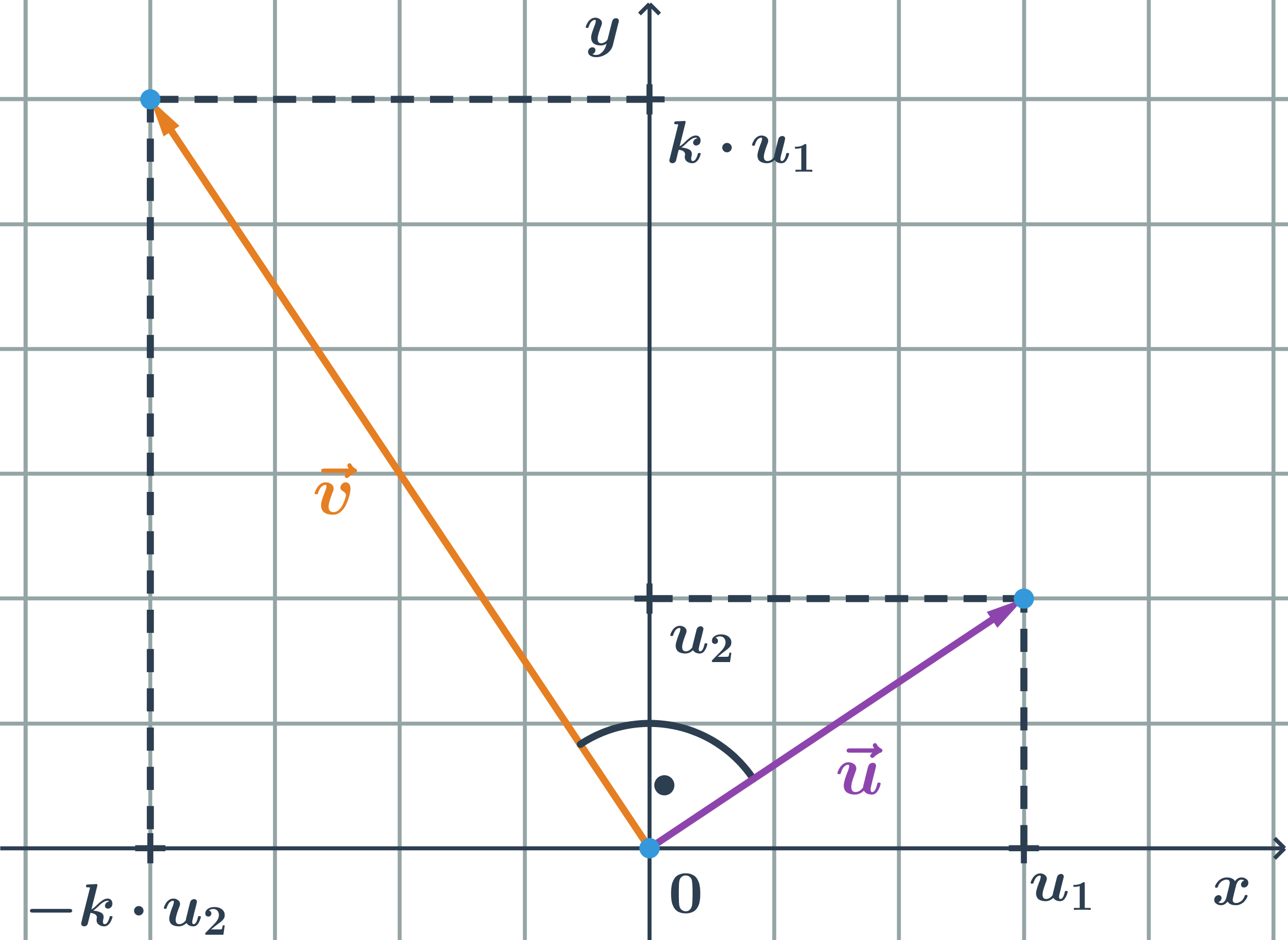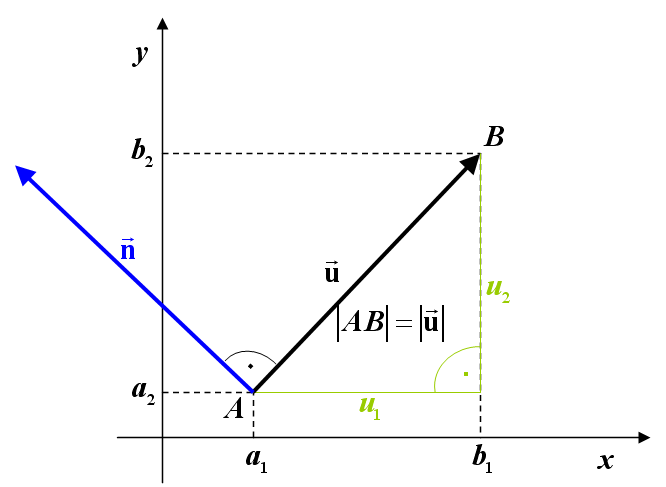
Při daném směrovém vektoru nám k získání vektoru normálového stačí prohodit souřadnice a u jedné z nich změnit znaménko.Každá přímka v rovině je určena dvěma různými body A a B. Tyto body určují také vektor. My tento vektor pojmenujeme a využijeme jej pro zavedení parametrického vyjádření přímky. Jestliže A, B jsou dva různé body, pak vektor u = B – A nazýváme směrový vektor přímky AB.Obecná rovnice přímky v rovině má tvar: a x + b y + c = 0 ax+by+c=0 ax+by+c=0, kde konstanty a a b jsou souřadnice normálového vektoru a c reálné číslo.

Jak zjistit jestli bod leží na přímce : Body A, B, C leží na jedné přímce, právě tehdy, když je vektor AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC.
Jak normalizovat vektor
Délka vektoru se vypočte pomocí Pythagorovy věty. Pro normalizaci vektoru se vektor vydělí svojí délkou a získá se tak jednotkový (normalizovaný) vektor.
Jak se počítají vektory : Pokud chceme sčítat nebo odečítat vektory, prostě vezmeme jejich jednotlivé složky x-ové a y-ové. A ty buď sečteme nebo od sebe odečteme.
Směrnice přímky je číslo měřící strmost dané přímky. Matematicky směrnici spočítáme jako "změna y dělená změnou x" (přesněji změna y-ové souřadnice dělená změnou x-ové souřadnice při přechodu mezi dvěma libovolnými body ležícími na dané přímce).
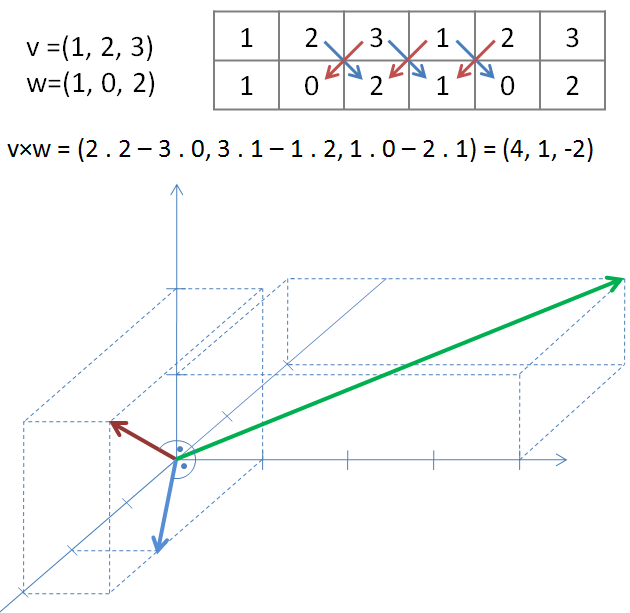
Kdybychom chtěli spočítat úhel mezi vektory u a v, tak víme, že pro něj platí kosinus fí však rovná se skalární součin vektoru u a v děleno velikost vektoru u krát velikost vektoru v.
Co když rovnice nemá řešení
Soustava nemá žádné řešení – po dosazení se ve vzniklé rovnici odečte i druhá neznámá a vznikne neplatná rovnost. Soustava má nekonečně mnoho řešení – po dosazení se ve vzniklé rovnici odečte i druhá neznámá a vznikne platná rovnost.Odchylka přímky a roviny
Je-li přímka p kolmá k rovině ρ, je jejich vzájemná odchylka φ = π/2. Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ. Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q.1) Vzhledem k tomu, že známe souřadnice středu kružnice a poloměr, stačí sestavit středovou rovnici kružnice: k: (x-1)^2+(y-2)^2=4 (nulové body jsou x-ové a -yové souřadnice středu, 4 je poloměr^2. Poté stačí obrázek a je vidět, že K je vnitřním bodem a M leží na kružnici.
Definice normy a úhlu vektorů
Nechť V je reálný vektorový prostor se skalárním součinem f. ‖v‖=√f(v,v). Vektor v se nazývá normovaný (jednotkový), je-li ‖v‖=1. Jinak řečeno, norma vektoru je odmocnina ze skalárního součinu tohoto vektoru samého se sebou.
Jak se určuje velikost vektoru : Velikost vektoru u je velikost kterékoliv orientované úsečky určující vektor u. Velikost vektoru u označujeme symbolem |u|. Jestliže |u| = 1, nazývá se vektor u jednotkový vektor.
Jak se počítá velikost vektoru : Výpočet velikosti vektoru je odvozen z výpočtu přepony pomocí Pythagorovy věty. Velikost vektoru u značíme absolutní hodnotou |u|. Častou chybou při výpočtu velikosti vektoru je nesprávné umocňování záporného čísla.
Jak vypočítat směrnici Tečny
Směrnice tečny ke grafu je dána kT = f ′(a), aby tato přímka i křivka měly v daném bodě stejný směr. Dostaneme tak rovnici tečny: y − f (a) = f ′(a)⋅(x − a).
Pro směrnici k přímky p platí k=tgα, kde α je úhel, který svírá přímka p s kladným směrem osy x. Číslo q je pak y-ová souřadnice průsečíku přímky p s osou y.Definice normy a úhlu vektorů
Vektor v se nazývá normovaný (jednotkový), je-li ‖v‖=1. Jinak řečeno, norma vektoru je odmocnina ze skalárního součinu tohoto vektoru samého se sebou. Nechť V je reálný vektorový prostor se skalárním součinem f. cosφ=f(u,v)‖u‖‖v‖,0≤φ≤π.
Jak se sčítají vektory : Sčítáme-li dva vektory, tak prostě a jednoduše sečteme jejich x-ové složky a jejich y-ové složky. A tak dostaneme výsledný vektor.