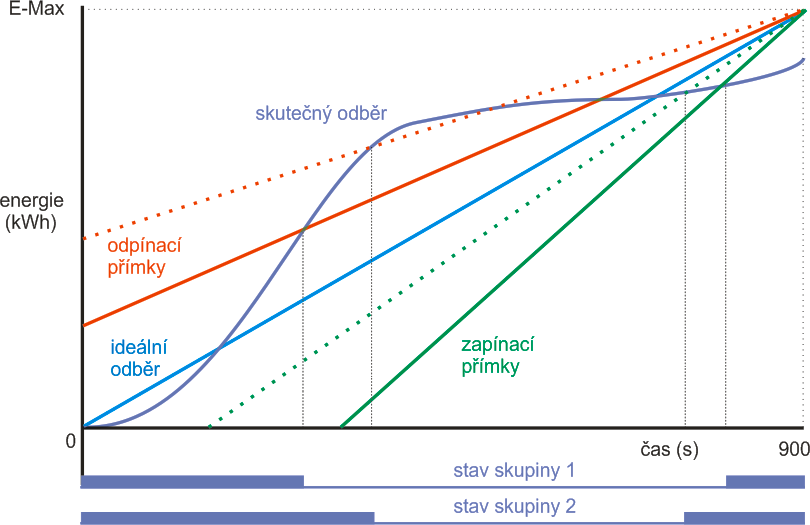
Nalezení extrému funkce
Pokud je první nenulová derivace v tomto bodě lichá, pak extrém nenastává, jedná se o inflexní bod. Pokud je první nenulová derivace v tomto bodě sudá a je větší než nula, pak nastává minimum; pokud je menší než nula nastává maximum.Maximum funkce
Hledání (globálního) maxima resp. minima funkce je základní úlohou optimalizace v matematice. (Globální) maximum funkce f(x) : M → R na množině M je bod y ∈ M takový, že f(y) ≥ f(x) pro všechna x ∈ M.Platí tak:
- Pokud má funkce f v bodě x extrém, tj. minimum nebo maximum, a pokud v tomto bodě existuje derivace (!), pak je tato derivace nulová.
- Pokud má funkce f v bodě x nulovou derivaci, pak v tomto bodě může být extrém, ale také nemusí.
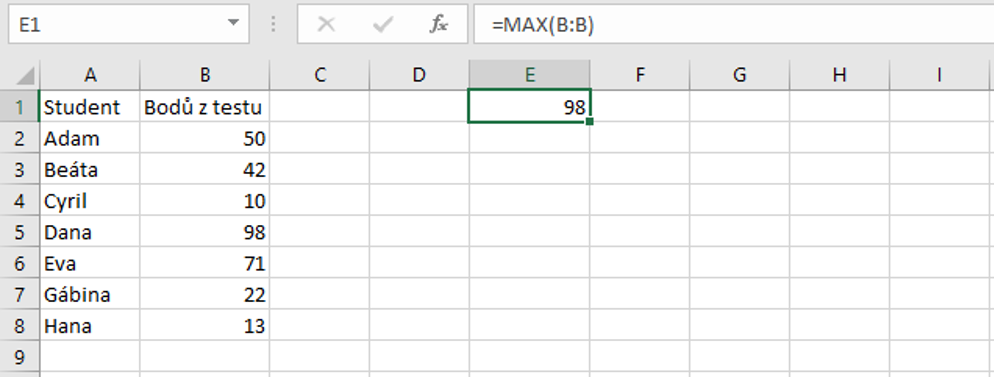
V jakém bodě má funkce minimum : Poznámka: Funkce má ostré lokální minimum v bodě x = 0.
Co je to minimum funkce
Minimum je matematická funkce, jejíž funkční hodnota představuje nejnižší hodnotu ze všech vstupních parametrů. Funkce provádí porovnání jednotlivých parametrů a výsledkem je hodnota toho parametru, který se při porovnání se všemi ostatními jeví jako nejnižší.
Co je lokální extrém : Lokální extrémy jsou body, v nichž funkce nabývá vzhledem k jejímu okolí největší nebo nejmenší hodnoty. V těchto bodech se funkce mění z rostoucí na klesající či naopak z klesající na rostoucí.
Jak zjistíme vrchol paraboly Souřadnice vrcholu paraboly jednoduše zjistíme díky vzorečku -b/2a. Na základě tohoto vzorce zjistíme x-ovou souřadnici vrcholu a y-ovou spočítáme pouhým dosazením do předpisu funkce.

Předpis lineární funkce je f:y=ax+b. Pomocí koeficientů a a b můžeme ovlivnit vzhled grafu lineární funkce, jestli bude funkce rostoucí, nebo klesající a kde graf protne osu y. f:y=ax+b, kde a a b jsou reálná čísla.
Co to je extrém
Extrém označuje krajnost, výstřednost, mimořádnost.Derivace je důležitý pojem matematické analýzy a základ diferenciálního počtu. Derivace funkce je změna (růst či pokles) její hodnoty v poměru ke změně jejího argumentu, pro velmi malé změny argumentu. Výpočet derivace se nazývá derivování. Opačným procesem k derivování je integrování.Extrémy funkce tří proměnných
Pokud druhou derivaci dvakrát podle x označíme jako D1, platí pro extrémy následující pravidla: Pokud je D1<0, D2>0, D3<0, tak se jedná o lokální maximum. Pokud je D1>0, D2>0, D3>0, tak se jedná o lokální minimum. Ve všech ostatních případech se o lokální extrém nejedná.
nejvyšší {sup.}
Jak zjistit minimum kvadratické funkce : Grafem kvadratické funkce y=a⋅x2b⋅xc je křivka, které říkáme parabola. Je-li a0 , má minimum (je otevřená směrem nahoru), je-li a0 , má maximum (je otevřená směrem dolů). Extrém (minimum/maximum) zjistíme úpravou předpisu do tvaru y=x−m2n .
Jak najít lokální extrémy : Extrémy funkce tří proměnných
Pokud druhou derivaci dvakrát podle x označíme jako D1, platí pro extrémy následující pravidla: Pokud je D1<0, D2>0, D3<0, tak se jedná o lokální maximum. Pokud je D1>0, D2>0, D3>0, tak se jedná o lokální minimum. Ve všech ostatních případech se o lokální extrém nejedná.
Jak Vypocitat vrchol
Jak zjistíme vrchol paraboly Souřadnice vrcholu paraboly jednoduše zjistíme díky vzorečku -b/2a. Na základě tohoto vzorce zjistíme x-ovou souřadnici vrcholu a y-ovou spočítáme pouhým dosazením do předpisu funkce.
Asi nejjednodušší je použít vzorec pro výpočet souřadnic vrcholu. Vzorec říká, že x-ová souřadnice vrcholu je minus b lomeno dvě a, kdy a je parametr u x na druhou a b je parametr u x.Nyní si můžeme funkci zavést přesnou definicí: "Funkce je předpis, který každému x z definičního oboru přiřazuje právě jednu funkční hodnotu y." Pro definici funkce je velmi důležitá část, kdy jednomu x přiřazujeme pouze jednu funkční hodnotu.
Jak určit předpis funkce : Předpis lineární funkce je f:y=ax+b. Pomocí koeficientů a a b můžeme ovlivnit vzhled grafu lineární funkce, jestli bude funkce rostoucí, nebo klesající a kde graf protne osu y. f:y=ax+b, kde a a b jsou reálná čísla.