
Každý úhel má svou osu, což je přímka, která prochází vrcholem úhlu a daný úhel půlí. Už z této definice vyplývá, že osa úhlu je v každém svém bodu stejně vzdálená od prvního a druhého ramene. Osa se obvykle značí malým písmenem o.Osová souměrnost O(o) s osou o je zobrazení v rovině, ve kterém se zobrazí každý bod X \in o na bod X'=X a každý bod X \not\in o na bod X' tak, že úsečka XX' je kolmá na osu o a střed S úsečky XX' leží na přímce o. Tedy platí, že |XS|=|SX'|, kde bod S \in o. Přímka o se nazývá osa souměrnosti.Narýsovaný úhel vystřihni (celou část, která se vejde na papír) a přeložením najdi jeho osu souměrnosti (přímku, která rozdělí úhel na dvě stejné, souměrné poloviny). Nalezenou osu vytáhni tužkou a pomocí úhloměru zkontroluj, že rozděluje úhel na dvě stejné poloviny.
Jak se značí osa : Taková kružnice má střed So, poloměr |SoA| a nazývá se opsaná, značíme ko.
Co to je osa v geometrii
Osa, též symetrála, je přímka určující souměrnost množiny bodů nebo tělesa. Množina bodů je osově souměrná podle přímky p, jestliže s každým bodem obsahuje také jeho obraz souměrný podle osy p. Dva body jsou souměrné podle dané osy, jestliže jimi určená úsečka je kolmá na osu a její střed leží na ose.
Co to je osa úsečky : Střed úsečky je bod, který leží na úsečce a jehož vzdálenost od obou krajních bodů je stejná. Osa úsečky je přímka kolmá k úsečce procházející jejím středem. Všechny body na ose úsečky mají od obou krajních bodů stejnou vzdálenost. Úsečka je středově souměrná podle svého středu.
Střed úsečky dělí úsečku na dvě stejné části. Pokud leží krajní body úsečky A B AB AB na číselné ose a jejich polohám odpovídají hodnoty a a b, potom jejímu středu S odpovídá číslo s = a + b 2 s=\frac{a+b}{2} s=2a+b.

- Přiložíme pravítko k úsečce tak, aby 0 překrývala krajní bod úsečky (bod A)
- Délku úsečky zjistíme na pravítku u jeho krajního bodu.
- Velká čísla na pravítku znamenají centimetry (cm), malé dílky jsou pak milimetry (mm)
Jak se graficky sčítají úhly
Úhly postupně přeneseme: → Narýsujeme si polopřímku AL → Na polopřímku přeneseme úhel α → Vniklou polopřímku nazveme AM → Na polopřímku AM přeneseme úhel β tak, aby rameno AM bylo spoleně, ale jinak úhly neměli žádné společné body → Vzniklý úhel NAL je grafickým součtem úhlů α a β.2. Jak sestrojíme úhel 60°
- Přímka p a bod A.
- Oblouk kružnice z bodu A → vznikne bod X(na přímce p)
- Oblouk kružnice z bodu X stejné velikosti(tzn. o stejném poloměru jako oblouk z bodu A) → vznikne bod Y.
- Rameno AY → sestrojili jsme úhel YAX = 60°
OSA – Ochranný svaz autorský pro práva k dílům hudebním, z.s. (dále jen OSA) je spolek, který získal od ministerstva kultury České republiky statut tzv. kolektivního správce s oprávněním licencovat mj. veřejné hudební produkce.
Obdélník je v obecném případě osově souměrný podle dvou os. Osami souměrnosti jsou rovnoběžky se stranami procházející průsečíkem úhlopříček. Speciální případ obdélníku – čtverec – je osově souměrný podle čtyř os, dalšími dvěma osami jsou jeho úhlopříčky.
Jak se dělá osova Soumernost : Odpovídající si body leží na kolmici k ose souměrnosti v opačných polorovinách a ve stejné vzdálenosti od osy. Osovou souměrnost můžeme zapsat: O(o): A → A'. Čteme: obrazem bodu A v osové souměrnosti je bod .
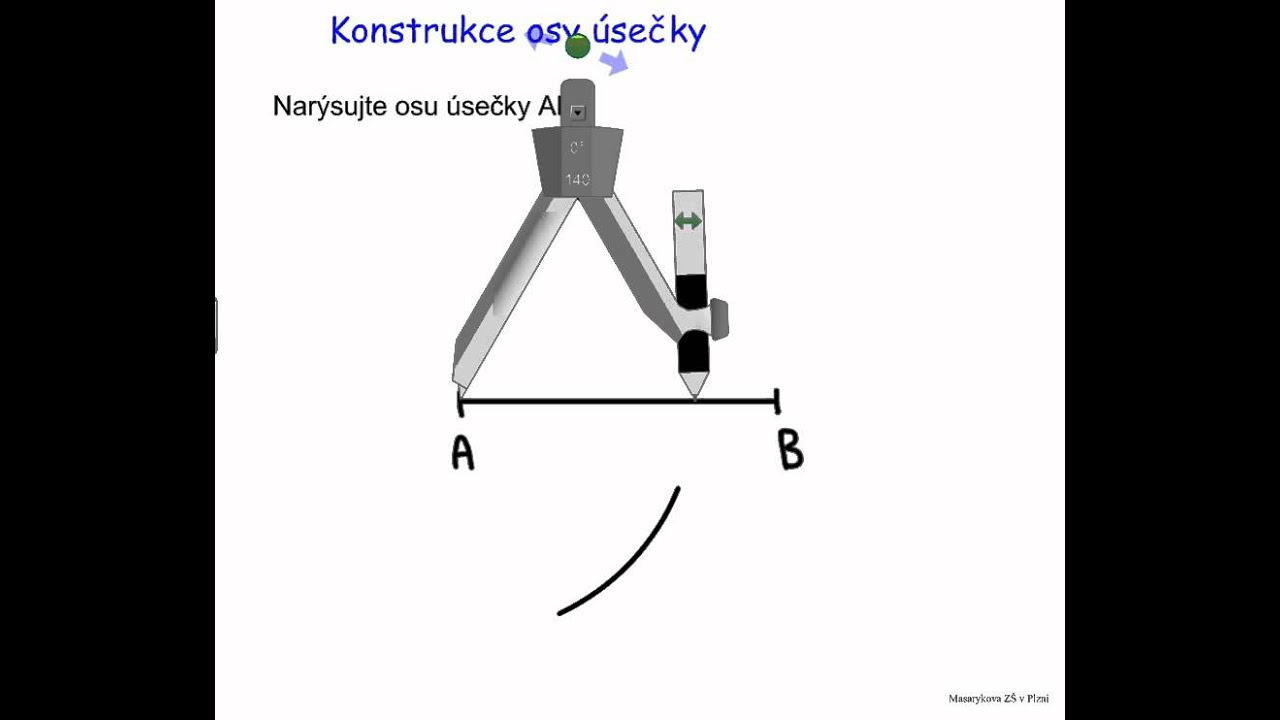
Jak se dělá střed úsečky : Způsobů je několik, ale nejklasičtější je protnutí dvou kružnic se stejným poloměrem, větším než je polovina úsečky, a se středy na koncích úsečky. Spojnice těchto průsečíků je k přímce kolmá a půlí ji (prochází středem).
Jak zjistit střed úsečky
Způsobů je několik, ale nejklasičtější je protnutí dvou kružnic se stejným poloměrem, větším než je polovina úsečky, a se středy na koncích úsečky. Spojnice těchto průsečíků je k přímce kolmá a půlí ji (prochází středem).
Střed úsečky je „průměrem“ jejích krajních bodů.Střed úsečky je bod, který leží na úsečce a jehož vzdálenost od obou krajních bodů je stejná. Osa úsečky je přímka kolmá k úsečce procházející jejím středem. Všechny body na ose úsečky mají od obou krajních bodů stejnou vzdálenost. Úsečka je středově souměrná podle svého středu.
Jak se dělí úhel : Druhy úhlů
- Nulový úhel (0°, 0 rad) je úhel, jehož ramena leží na sobě.
- Ostrý úhel (< 90°, < /2 rad) je úhel menší než pravý úhel.
- Pravý úhel (90°, /2) je polovina přímého úhlu.
- Tupý úhel (> 90°, ale < 180°) je úhel větší než pravý úhel, ale menší než přímý úhel.
- Přímý úhel (180°,
- Plný úhel (360°, 2.





