tvar koule – míč, kulový kryt lampy, tvar kvádru – krabička od sirek, panelový dům s vodorovnou střechou, tvar válce – hrneček. Je důležité, aby si žáci uvědomili, že i třída, různé místnosti mají v podstatě tvar kvádru, pokud pomineme různé výklenky a otvory oken a dveří.Krychle je prostorový útvar, který má šest stěn, tvar každé stěny je čtverec. Všechny hrany krychle mají stejnou délku a všechny vnitřní úhly jsou pravé, tedy jejich velikost je 90°. Příklady krychle v běžném životě zahrnují kostky cukru nebo Rubikovu kostku.Kvádr a krychle jsou speciální případy hranolu, jejich podstava je obdélník (čtverec) a výška je zbývající hrana. Objem kvádru je tedy součin délek jeho hran: V = a b c V = abc V=abc. Objem krychle vypočítáme stejným způsobem.
Jak se počítá výška kvádru : Výška v kvádru je rovna trojnásobku délky kratšího rozměru podstavy.
Kolik má kvádr stěnových úhlopříček
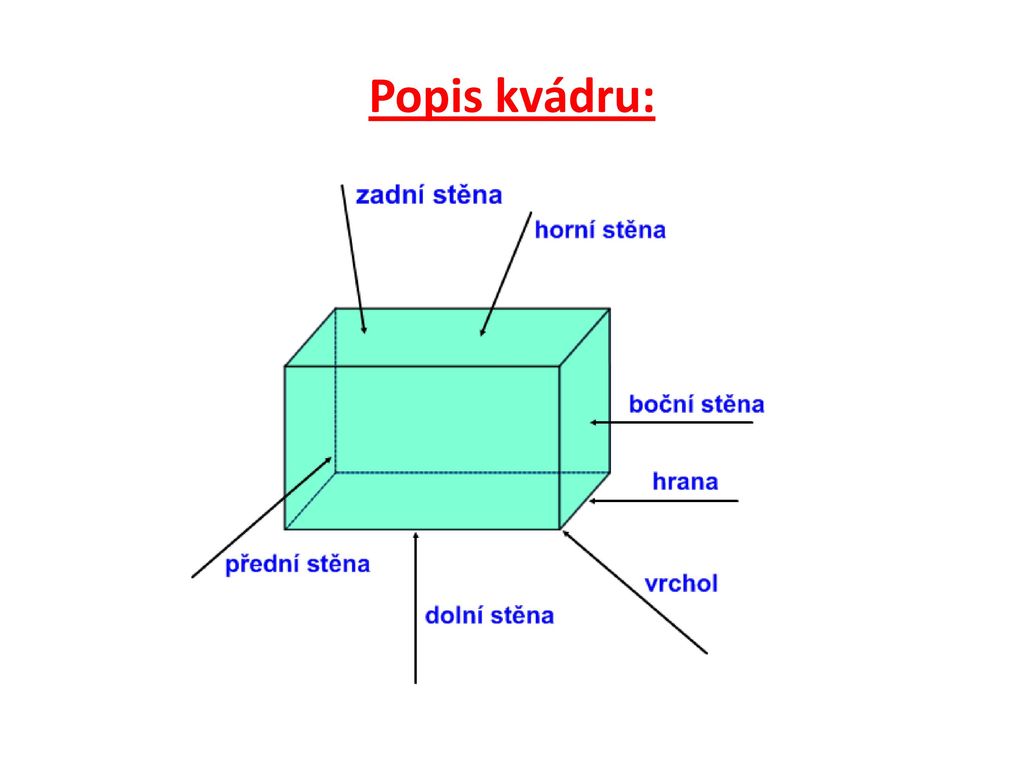
Kvádr má osm vrcholů, dvanáct hran, šest stěn, dvanáct stěnových úhlopříček, čtyři tělesové úhlopříčky.
Jak vypada kvádr : Kvádr má šest stěn obdélníkového tvaru (ve speciálních případech 2 čtvercové + 4 obdélníkové nebo 6 čtvercových) z nichž dvě protilehlé jsou vždy shodné, osm vrcholů a dvanáct hran z nichž čtveřice rovnoběžných má vždy shodnou délku.
Hrany: Krychle má celkem dvanáct hran, které jsou rovnoběžné a spojují vrcholy. Vrcholy: Krychle má osm vrcholů, které jsou místa, kde se střetávají tři hrany. Povrchová plocha: Celková plocha povrchu krychle, která se skládá z šesti čtvercových stěn. Povrchová plocha se spočítá pomocí vzorce: P = 6a^2.
Kvádr má šest stěn obdélníkového tvaru (ve speciálních případech 2 čtvercové + 4 obdélníkové nebo 6 čtvercových) z nichž dvě protilehlé jsou vždy shodné, osm vrcholů a dvanáct hran z nichž čtveřice rovnoběžných má vždy shodnou délku.
Jak se vypočítá kvádr
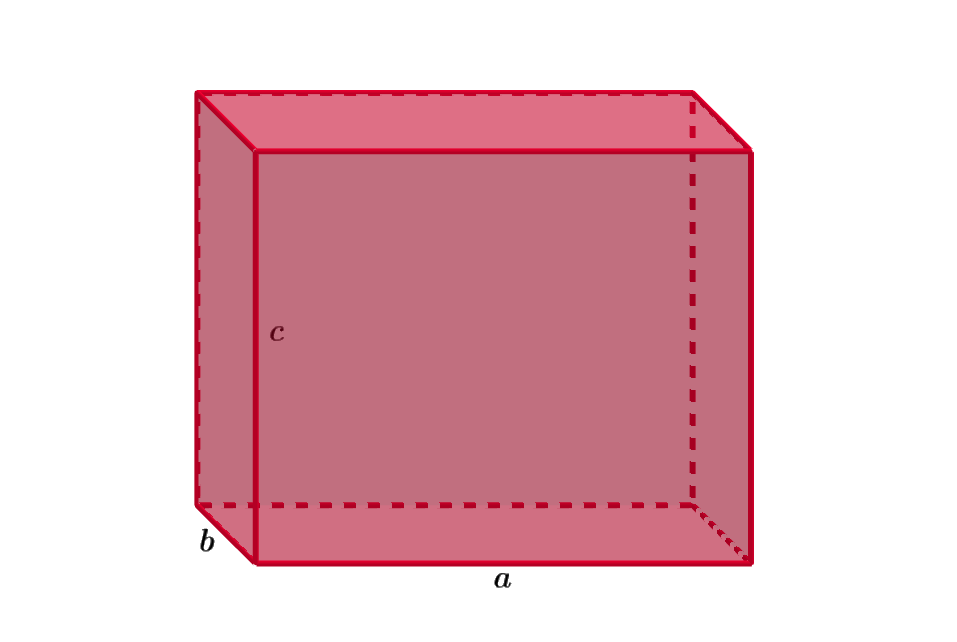
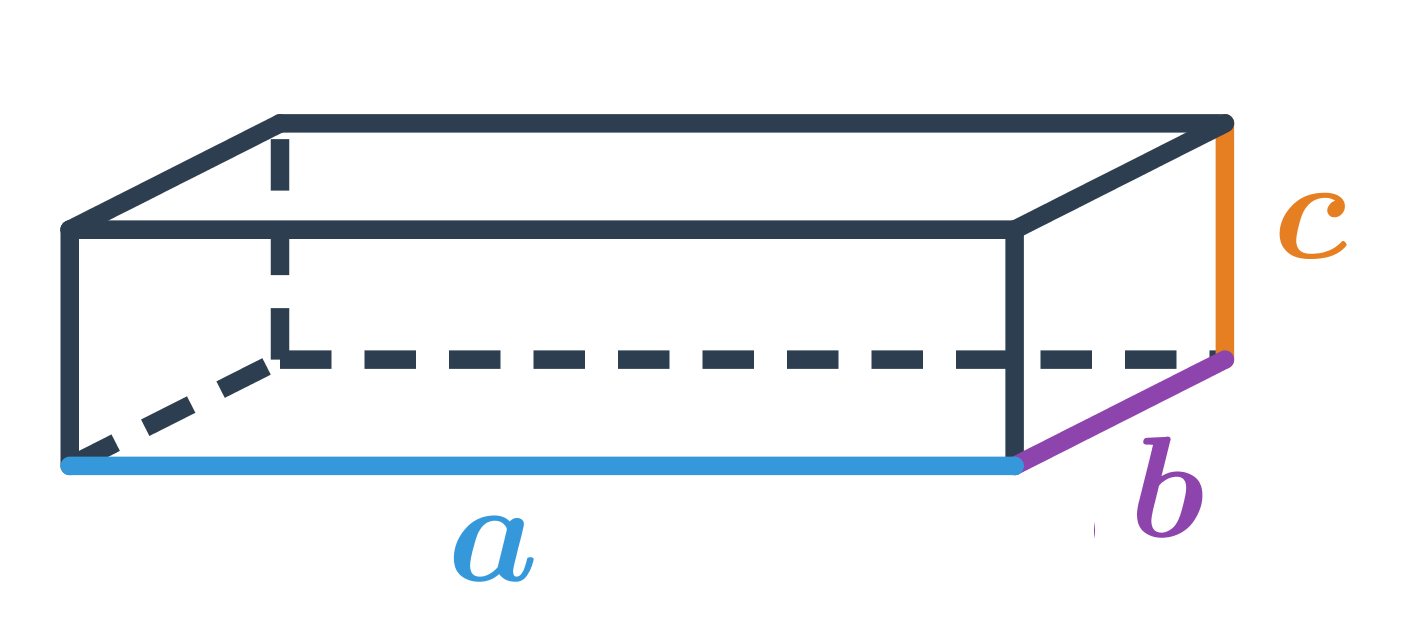
U kvádru můžou být všechny tři rozměry různé (délka, šířka a výška), proto těmto rozměrům obecně přiřazujeme tři různá písmenka – „a, b, c“. Objem kvádru vypočítáme tak, že spočteme obsah podstavy (obdélník – S=a.b), kterou dále vynásobíme výškou kvádru (c).Obsah kvádru se počítá jako délka hrany [a] x délka hrany [b] x délka hrany [c].Síť kvádru se skládá ze všech jeho šesti stěn (obr. 3.8.2). V =abc. S =2ab+2(ac+bc)=2(ab+ac+bc).
Kvádr je prostorové těleso, jehož podstavou je čtverec nebo obdélník a boční stěny jsou kolmé na podstavu. Dvě protější stěny jsou stejné. Kvádr má osm vrcholů, dvanáct hran, šest stěn, dvanáct stěnových úhlopříček, čtyři tělesové úhlopříčky.
Kolik bočních stěn má kvádr : Kvádr má šest stěn obdélníkového tvaru (ve speciálních případech 2 čtvercové + 4 obdélníkové nebo 6 čtvercových) z nichž dvě protilehlé jsou vždy shodné, osm vrcholů a dvanáct hran z nichž čtveřice rovnoběžných má vždy shodnou délku.
Kolik má kvádr vrcholů : Kvádr má šest stěn obdélníkového tvaru (ve speciálních případech 2 čtvercové + 4 obdélníkové nebo 6 čtvercových) z nichž dvě protilehlé jsou vždy shodné, osm vrcholů a dvanáct hran z nichž čtveřice rovnoběžných má vždy shodnou délku.
Jak se počítá obsah stěny krychle
Vzorce pro výpočet povrchu krychle
Obsah jedné stěny tj. jednoho čtverce vypočítáme jednoduše podle vzorce [S] = a × a. Výsledek následně vynásobíme šesti a tak získáme povrch krychle. Zjednodušení výpočtového vzorce: [S] = 6 × a × a => 6 × a2.
| Krychle | |
|---|---|
| Počet vrcholů | 8 |
| Počet hran | 12 |
| Počet stěn | 6 |
| Úhel u vrcholu | 90° |
KVÁDR. Za kvádr považujeme kolmý hranol, jehož podstavou je obdélník nebo čtverec. Tudíž se jedná o čtyřboký hranol.
Jak se vypočítá obsah kvádru : Pro výpočet obsahu kvádru stačí znát délky tří jeho stran. Do kalkulačky tedy zadejte šířku kvádru a, délku kvádru b a výšku kvádru c. Obsah kvádru se počítá jako délka hrany [a] x délka hrany [b] x délka hrany [c].