Definice odchylky přímek v planimetrii:
Odchylka dvou různoběžných přímek je velikost každého z ostrých nebo pravých úhlů, které spolu přímky svírají.Mají-li dvě různé roviny společný bod, pak mají společnou přímku, která tímto bodem prochází, kromě této přímky nemají žádné další společné body (pokud nejsou roviny totožné). Společnou přímku p dvou různoběžných rovin nazýváme průsečnice.Odchylka dvou vektorů
Pro dva nenulové vektory u, v v rovině nebo v prostoru a jejich odchylku φ platí: uv = |u|⋅|v| cos φ, φ ∈ <0°; 180˚>.
Jak vypočítat průsečík dvou přímek : X = Q + sv, pro nějakou hodnotu parametrů t, s. Pokud hledáme průsečík těchto přímek, hledáme hodnoty parametrů t a s, pro které obě přímky určují stejný bod. Řešíme tedy rovnici P + tu = Q + sv.
Jak Vypocitat odchylku dvou rovin
Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ. Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q. Vztah mezi hledanou a získanou odchylkou je: φ = π/2 – α.
Jak se značí odchylka : Směrodatná odchylka, značená řeckým písmenem σ, je v teorii pravděpodobnosti a statistice často používanou mírou statistické variability.
Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ. Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q. Vztah mezi hledanou a získanou odchylkou je: φ = π/2 – α.
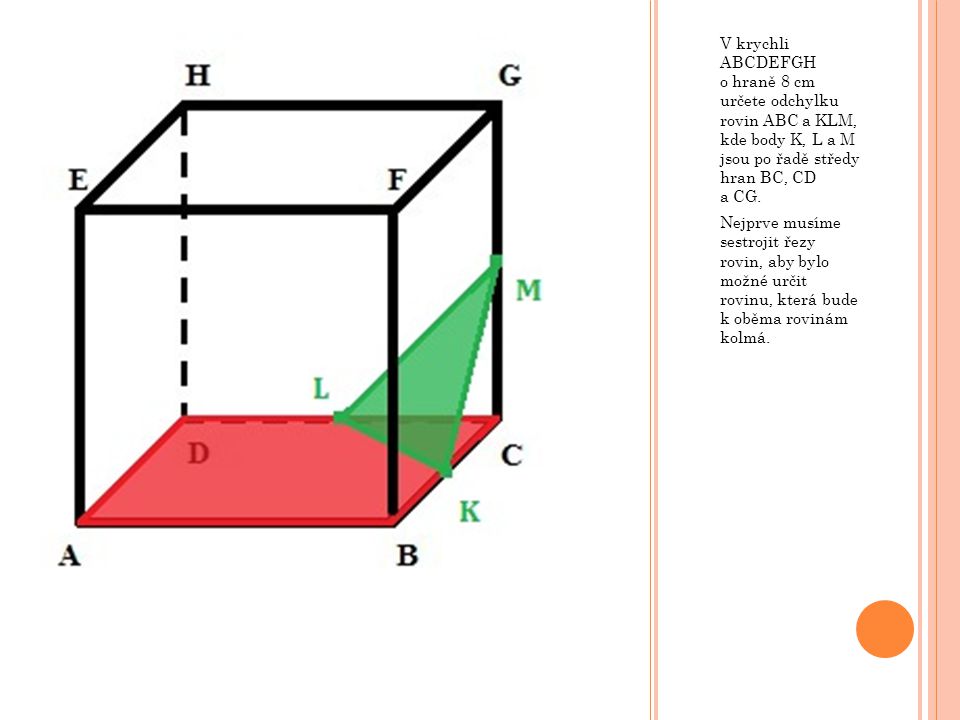
Postup při hledání průsečíku přímky s rovinou: • Sestrojíme řezy tělesa rovinou, zakreslíme přímku. obsahuje přímku. Sestrojíme průsečnici obou rovin. Průsečík průsečnice a přímky je hledaným bodem.
Jak se počítá standardní odchylka
Směrodatná odchylka
Informuje nás o tom, jak daleko jsou v průměru jednotlivé údaje rozprostřené kolem svého aritmetického průměru. Vypočítá se jako odmocnina z rozptylu a na rozdíl od rozptylu má stejný fyzikální rozměr jako původní veličina.Odchylka přímky a roviny
Je-li přímka p kolmá k rovině ρ, je jejich vzájemná odchylka φ = π/2. Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ. Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q.Kritérium kolmosti dvou rovin: Obsahuje-li rovina σ přímku p kolmou k rovině ρ, pak jsou roviny σ, ρ k sobě kolmé. Definice: Je-li přímka p kolmá k rovině ρ, pak její odchylka od ρ je 90°. Není-li p kolmá k ρ a je-li p1 pravoúhlý průmět p do ρ, nazýváme odchylkou přímky p od roviny ρ odchylku přímek p, p1.
Součet čtverců odchylek od průměru je možné zapsat jako \sum (x_i-\bar x)^2, kde n je počet hodnot a x_i tyto hodnoty označují. Průměr je popisná charakteristika v tom smyslu, že součet kladných a záporných odchylek od průměru je roven nule.
Co určuje směrodatná odchylka : Jako charakteristika přesnosti měření se téměř výhradně využívá směrodatná odchylka σ. Tu lze vypočítat jako kvadratický průměr skutečné chyby.
Jak vypočítat odchylku přímky od roviny : Odchylka přímky a roviny
Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ. Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q. Vztah mezi hledanou a získanou odchylkou je: φ = π/2 – α.
Kdy je přímka kolmá k rovině
Přímka a rovina jsou k sobě kolmé právě tehdy, když je přímka kolmá ke všem přímkám roviny.
Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ. Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q. Vztah mezi hledanou a získanou odchylkou je: φ = π/2 – α.Průměrná odchylka je součet absolutních hodnot rozdílu každého datového bodu a průměru datové sady, dělený počtem prvků v datové sadě.
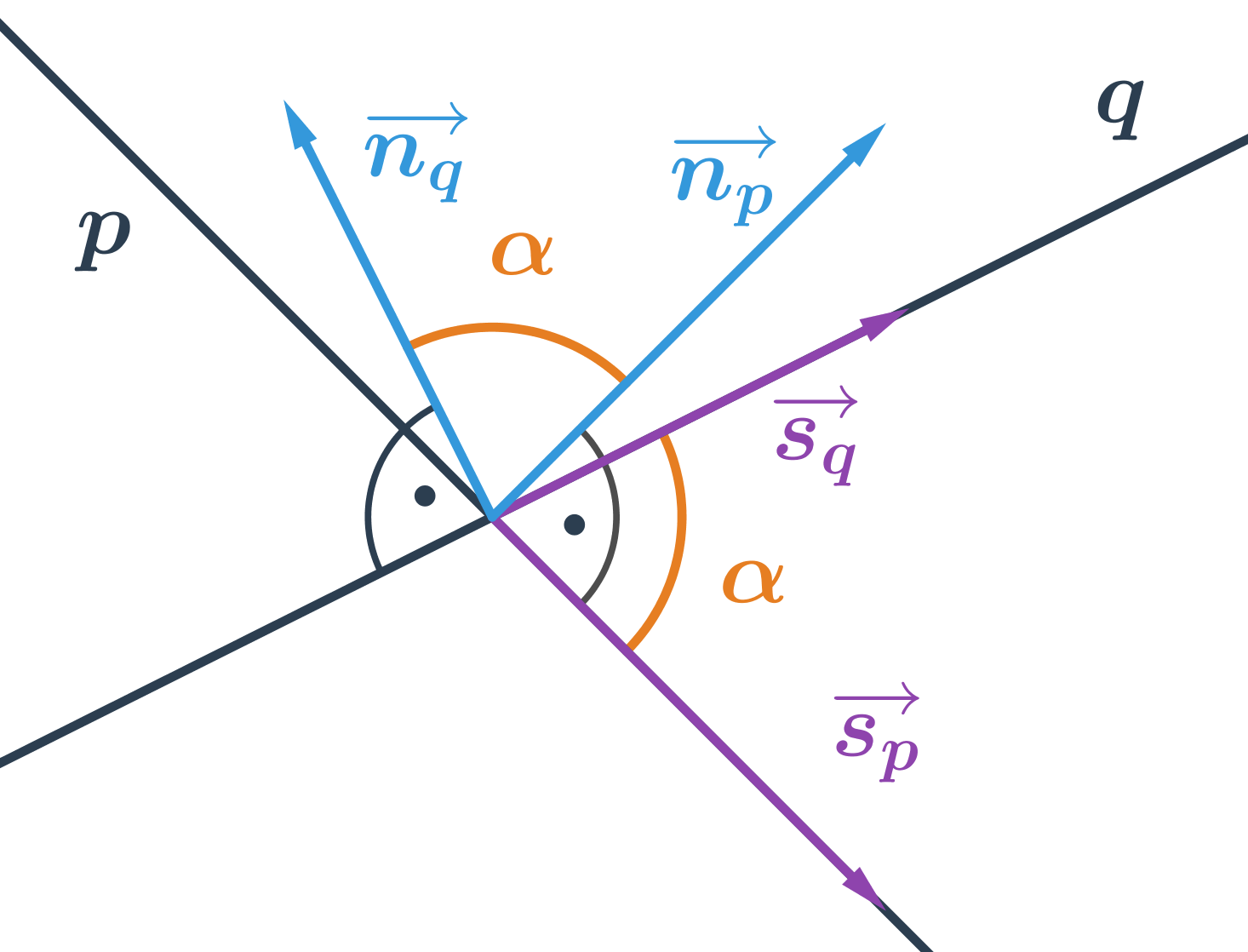
Jak určit odchylku dvou rovin : Odchylku dvou rovin můžeme tedy snadno určit pomocí jejich normálových vektorů. Pro výpočet odchylky φ dvou rovin ρ(A, nρ) a ψ(B, nψ) můžeme použít vzorec vyplývající z předchozí úvahy: \cosφ = \dfrac{|n_{ρ}n_{ψ}|}{|n_{ρ}||n_{ψ}|}, φ \in \langle 0°;90° \rangle.