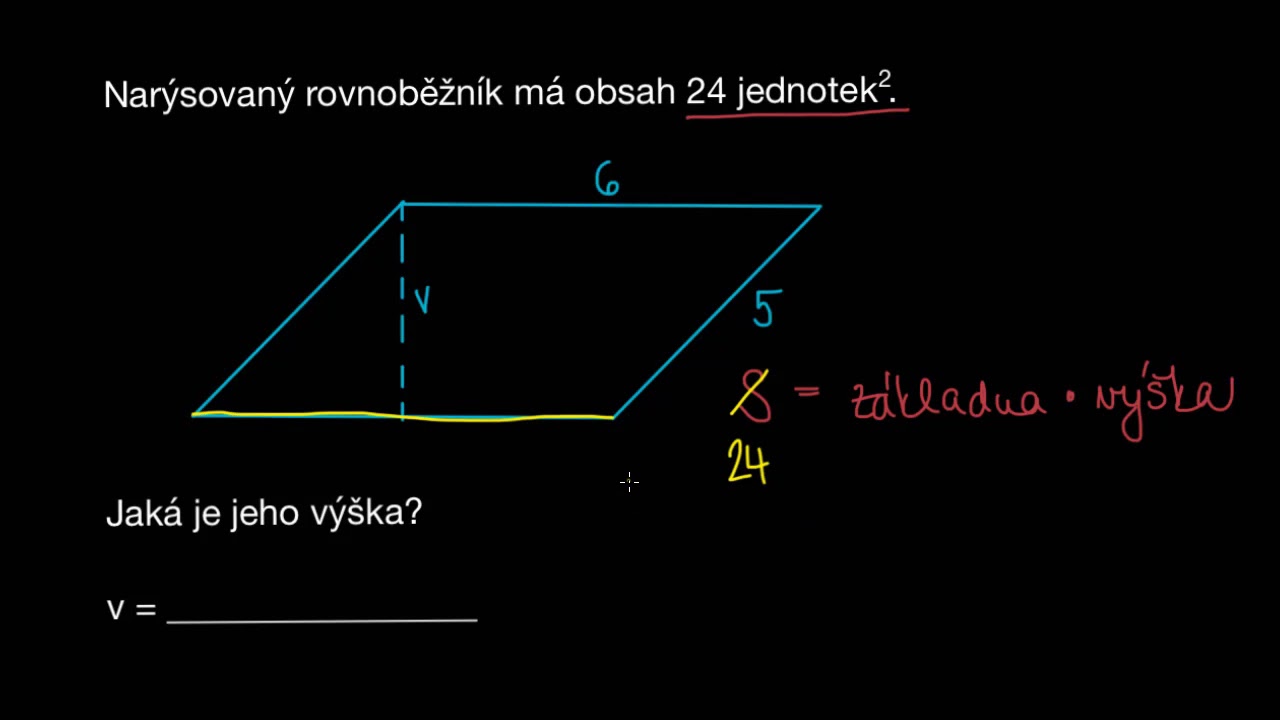
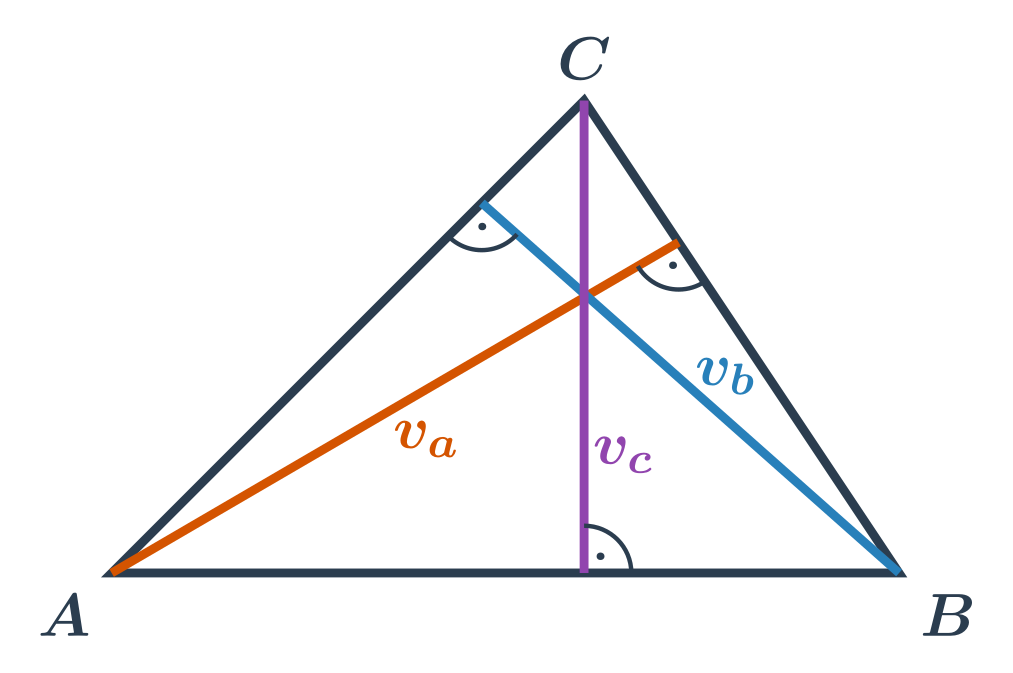
Výška v trojúhelníku je vlastně vzdálenost vrcholu od protější strany. Vzdálenost se měří vždy na kolmici, proto je to kolmice spuštěná z vrcholu na protější stranu.Vypocitejte jeho vysku. Jak se pocita to cviceni To je pythagorova věta – c^2=a^2+b^2, kde c je rameno, a je výška a b polovina základny (výška v rovnoramenném trojúhelníku půlí základnu).Výšky se rýsují celkem snadno, vezmete si pravítko a vedete kolmici ze strany c tak, aby tato kolmice procházela právě bodem C. Výšku můžeme vést z každého vrcholu trojúhelníka. Všechny výšky se pak protínají v bodě, které se nazývá průsečík výšek.
Co platí pro výšky v trojúhelníku : Každý trojúhelník má tři výšky. Menší straně odpovídá větší výška. Přímky, na nichž leží výšky, se protínají v jednom bodě, který se nazývá ortocentrum nebo také výšiště. Ortocentrum leží uvnitř trojúhelníku, pokud je ostroúhlý.
Co to je výška
Výška označuje obvykle vertikální vzdálenost dvou bodů, tj. nad určitou úrovní (vzhůru). Vzdálenost pod danou úrovní (dolů) bývá označována jako hloubka. Společně s délkou a šířkou slouží k určení rozměrů v trojrozměrném prostoru.
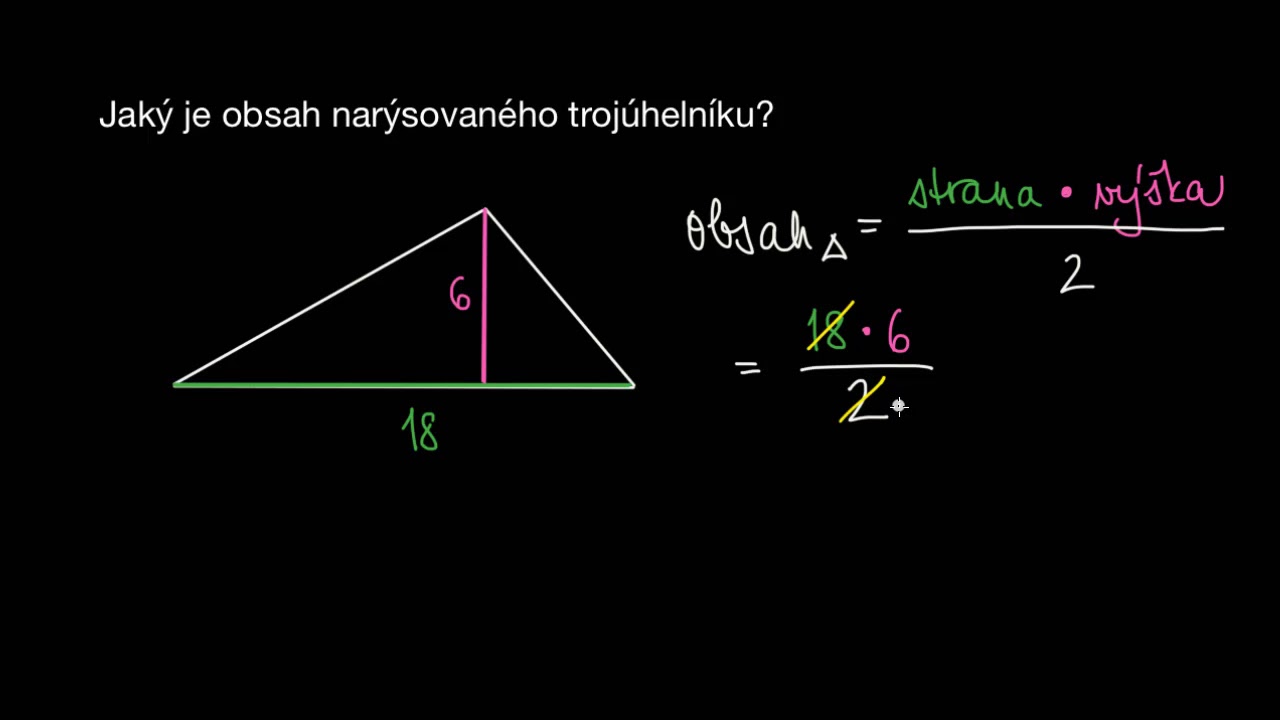
Jaký je vzorec pro obsah trojúhelníku : Pro výpočet obsahu trojúhelníku použijeme vzorec obsah = (strana krá výška)/2.
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
umime.to/FV2
Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami. Pythagorovu větu můžeme zapsat vztahem c 2 = a 2 + b 2 c^2 = a^2 + b^2 c2=a2+b2, kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.
Jak se značí výška
Výšky označujeme obvykle malým písmenem v s indexem názvu strany, ke které příslušná výška patří. Slovem výška označujeme v trojúhelníku jak úsečku, tak její délku. Konstrukce výšky trojúhelníku. Základem konstrukce výšky trojúhelníku je sestrojení kolmice k dané straně procházející protějším vrcholem.Pro výpočet obsahu trojúhelníku použijeme vzorec obsah = (strana krá výška)/2.Výška je vzdálenost bodu od nulové hladinové (referenční) plochy procházející nulovým výškovým bodem měřená podél svislice (ve směru siločar tíhového pole Země) = absolutní (nadmořská) výška. Relativní výška je vzdálenost bodu od jiné hladinové plochy než plochy nulové měřená podél svislice.
Výšky označujeme obvykle malým písmenem v s indexem názvu strany, ke které příslušná výška patří. Slovem výška označujeme v trojúhelníku jak úsečku, tak její délku. Konstrukce výšky trojúhelníku. Základem konstrukce výšky trojúhelníku je sestrojení kolmice k dané straně procházející protějším vrcholem.
Jak se vypočítá trojúhelník : Pro výpočet obsahu trojúhelníku použijeme vzorec obsah = (strana krá výška)/2.
Jak se počítá výměra obdélníku : Rozdělit místnost na obdélníky – v případě členitější místnosti je dobré si místnost rozdělit na několik částí, ideálně na obdélníky. Šířka a délka – změřte měřícím pásmem jednotlivé části a zaznamenejte si délku a šířku. Výpočet rozlohy – vynásobením délky a šířky jednotlivých částí se vypočítá rozloha v m2.
Jak se pocita Pythagora
Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.
Stoupněte si zády ke zdi, svěste paže, narovnejte záda, hlavu držte vzpřímeně. Rozkročte se, abyste mezi chodidly měli mezeru 10 až 15 cm. Udělejte značku na zdi ve výši bodu, kde končí klíční kost.Přibližná výška dítěte v dospělosti lze vypočítat podle následujícího návodu. K tělesné výšce rodiče stejného pohlaví přičteme výšku druhého rodiče zvětšenou (u chlapců) nebo zmenšenou (u dívek) o 13 cm. Součet poté vydělíme dvěma. Získáme nejpravděpodobnější dospělou výšku dítěte.
Jak se merila nadmořská výška : Odpověď: Nadmořská výška se obvykle měří ke střední (průměrné) hladině nejbližšího moře. v České republice (tedy vlastně v Rakousku-Uhersku a následně v Československu) se vycházelo až do roku 1955 ze střední výšky Jaderského moře v Terstu, od roku 1955 vycházíme ze střední hladiny Baltského moře.