Tangens úhlu α se rovná poměru délky protilehlé odvěsny ku délce přilehlé odvěsny. Tangens obvykle značíme buď t g tg tg nebo t a n tan tan.Goniometrické funkce na kalkulačce
- Stiskneme příslušnou funkci – sin, cos, tg.
- Napíšeme hodnotu úhlu.
- Stiskneme tlačítko rovná se.
- Výsledek je zapsán buď v podobě zlomku, případně v podobě desetinného čísla.
Goniometrické funkce a pravoúhlý trojúhelník
- Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony.
- Kosinus ( cos) úhlu α je poměr délky odvěsny přilehlé úhlu α a délky přepony.
- Tangens ( tan) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky odvěsny přilehlé úhlu α.
Jak vyjadrit tangens : Tangens. Tangens úhlu alfa se rovná poměru délky protilehlé odvěsny ku délce přilehlé odvěsny v pravoúhlém trojúhelníku. Tangens obvykle značíme buď tg nebo tan.
Kolik je tangens
Funkce tangens je definována v pravoúhlém trojúhelníku jako poměr protilehlé a přilehlé odvěsny. Jejím grafem je tangentoida. Funkce je definována v intervalu od 90 ° ± k · 180 ° do 270 ° ± k · 180 ° a nabývá hodnot od −∞ do +∞.
Co to je tangenta : V pravoúhlém trojúhelníku (pro ostrý úhel) je tangens úhlu definován jako poměr délek protilehlé a přilehlé odvěsny. Definici lze konzistentně rozšířit jak na reálná čísla, tak i do oboru komplexních čísel. Grafem tangenty v reálném oboru je transcendentní křivka tangentoida.
Kolik je tangens 60 stupňů OK tangens je protilehlá ku přilehlé protilehlá k úhlu 60 stupňů je 2 odmocniny ze 3 2 druhé odmocniny ze 3 a přilehlá je 2. Přilehlá k úhlu 60 stupňů je 2.
Nyní se budeme zabývat dalšími dvěma goniometrickými funkcemi tangens (značka tg) a kotangens (značka cotg).
Jak se počítá cotg
Funkce kotangens je definována v pravoúhlém trojúhelníku jako poměr přilehlé a protilehlé odvěsny.Tangens je goniometrická funkce. Je to funkce transcendentní, nelze ji obecně vyčíslit pomocí konečného počtu elementárních operací. Pro označení této funkce se obvykle používá značka tan (v českých publikacích běžně též tg) doplněná značkou nezávisle proměnné (zpravidla úhlu).Odhad periody.
Většina lidí zná vlastně jen čtyři takové funkce, jmenovitě sinus a kosinus se základní periodou 2π a tangens a kotangens se základní periodou π.
Dosadíme do pravé strany, kde tangens třiceti stupňů je přibližně roven 0,5773 (viz kalkulačka na počítání hodnoty funkce tangens). | c | = 3 0,577 3 = 5,196. Pro tangens třicet stupňů existuje tabulková hodnota, platí, že:
Kolik je tangens 2 :
| X [º] | X [rad] | tg(x) |
|---|---|---|
| 1 | 0,0175 | 0,0175 |
| 2 | 0,0349 | 0,0349 |
| 3 | 0,0524 | 0,0524 |
| 4 | 0,0698 | 0,0699 |
Kolik je síň 180 : Sinus a kvadranty
| Stupně | Radiány | sin (x) |
|---|---|---|
| 0° | 0 | 0 |
| 90° | π/2 | 1 |
| 180° | π | 0 |
| 270° | 3π/2 | −1 |
Kdy je tg 0
Tangens
| úhel | 0° | 180° |
|---|---|---|
| sinus úhlu | 0 | 0 |
| cosinus úhlu | 1 | -1 |
| tangens úhlu | 0 | 0 |
Sinus je goniometrická funkce nějakého úhlu. Zapisuje se jako sin θ, kde θ je velikost úhlu. Pro ostré úhly je definována v pravoúhlém trojúhelníku jako poměr protilehlé odvěsny a přepony (nejdelší strany). Definici lze konzistentně rozšířit jak na všechna reálná čísla, tak i do oboru komplexních čísel.Šína je obroučka, kroužek.
(Zároveň je šína pojem, který se používá hned v několika branžích, tak se nenechte zmást.)
Co ústí do právě síně : Žíly srdce
Dělíme na žíly ústící do koronárního sinu, žíly odvádějící krev z přední stěny pravé síně, do které následně ústí (venae ventriculi dextri anteriores) a malé žilky odvádějící krev do všech srdečních dutin (venae cordis minimae).






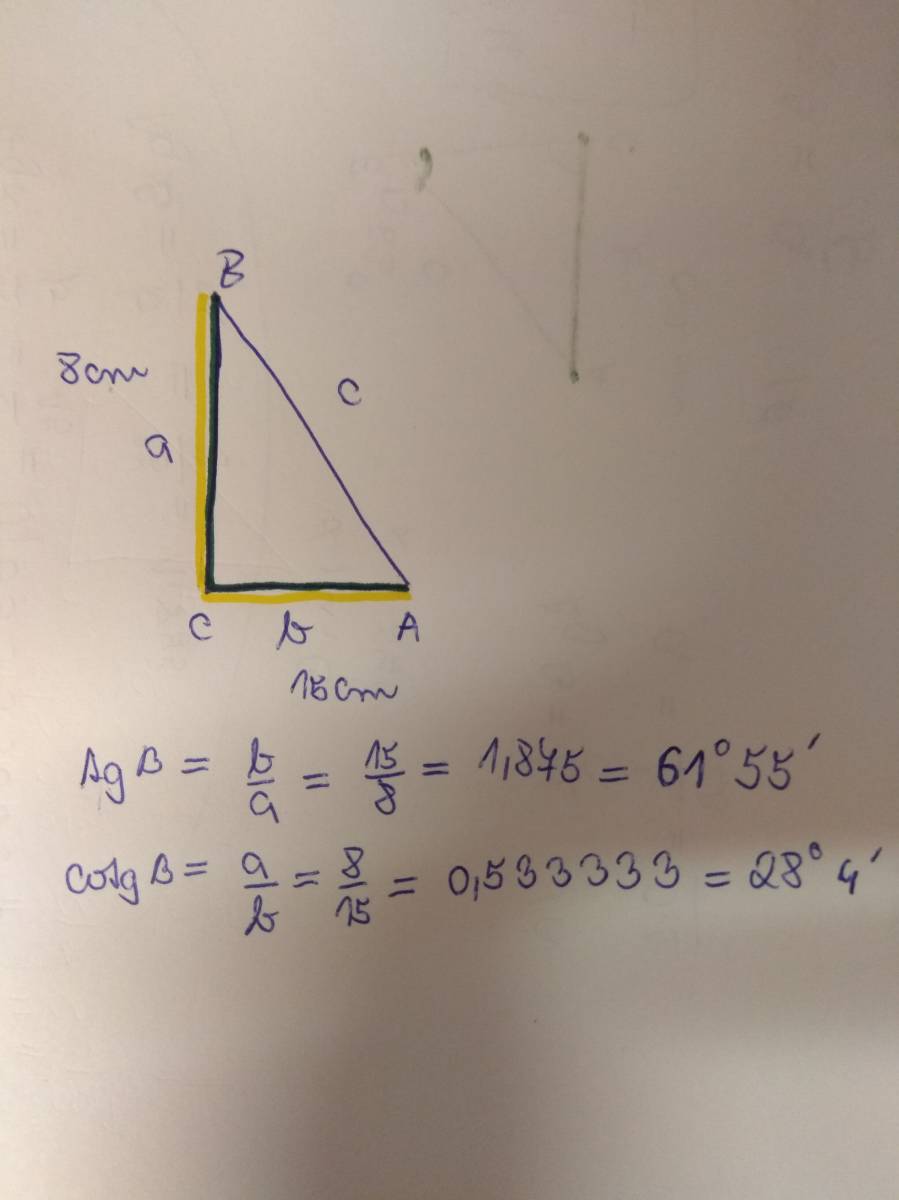
.png?bwg=1604855809)
