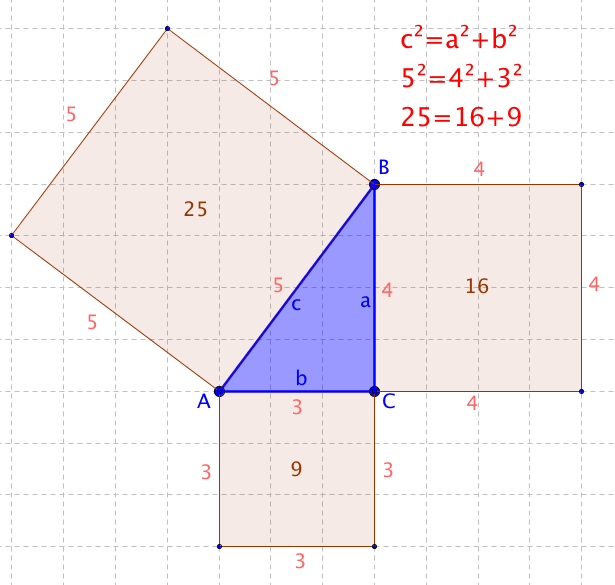
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .Vysvětlíme si, jak lze vypočítat délku strany trojúhelníku při zadaném obsahu a délce dvou dalších stran. Pro výpočet použijeme vzorec pro obsah trojúhelníku (strana krát výška)/2.Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.
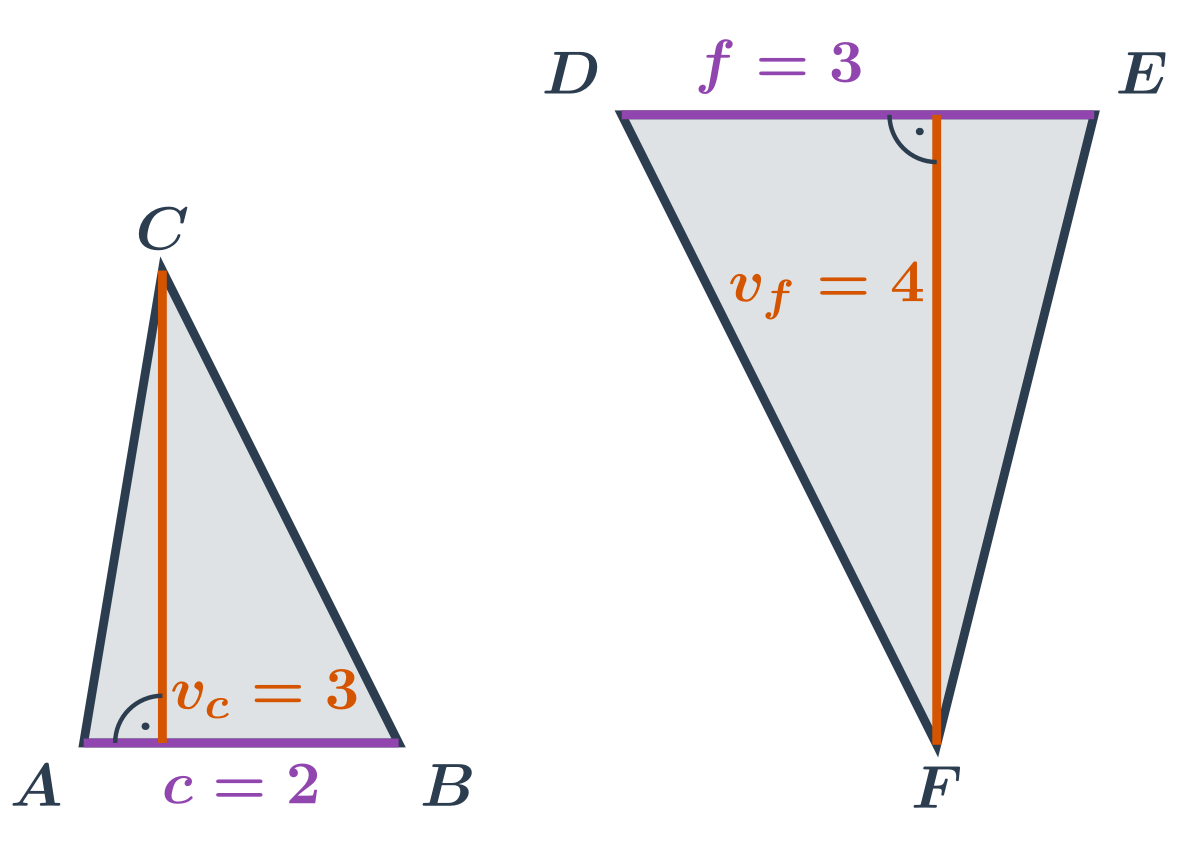
Jak se vypočítá trojúhelník : Pro výpočet obsahu trojúhelníku použijeme vzorec obsah = (strana krá výška)/2.
Jak se počítá přepona v pravoúhlém trojúhelníku
Platí Pythagorova věta
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců sestrojených nad jeho odvěsnami. Délku přepony pravoúhlého trojúhelníku vypočteme podle vzorce c2 = a2 + b2.
Jaký je vzorec pro obsah trojúhelníku : Trojúhelník je polovinou obsahu obdélníka, proto obsah trojúhelníka je jedna polovina x strana x výška (straně odpovídající): Pro výpočet obsahu trojúhelníka je možno použít libovolnou stranu s odpovídající výškou. Není ale možné použít stranu v kombinaci s jinou výškou.
Pythagorova věta: základní použití
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Pythagorova věta popisuje vztah, který platí mezi délkami stran pravoúhlého trojúhelníku. Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami.
Co rekl Pythagoras
Pythagorás ze Samu
První Řek, který si uvědomil, že Večerka i Jitřenka jsou jedna a tatáž planeta – Venuše. Prohlásil, že Země je kulatá a rozšířil Anaximandrův model sfér. V matematice proslul Pythagorovou větou pro pravoúhlý trojúhelník (kvadrát velikosti přepony je roven součtu kvadrátů velikostí odvěsen).Platí Pythagorova věta
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců sestrojených nad jeho odvěsnami. Délku přepony pravoúhlého trojúhelníku vypočteme podle vzorce c2 = a2 + b2.umime.to/FX2
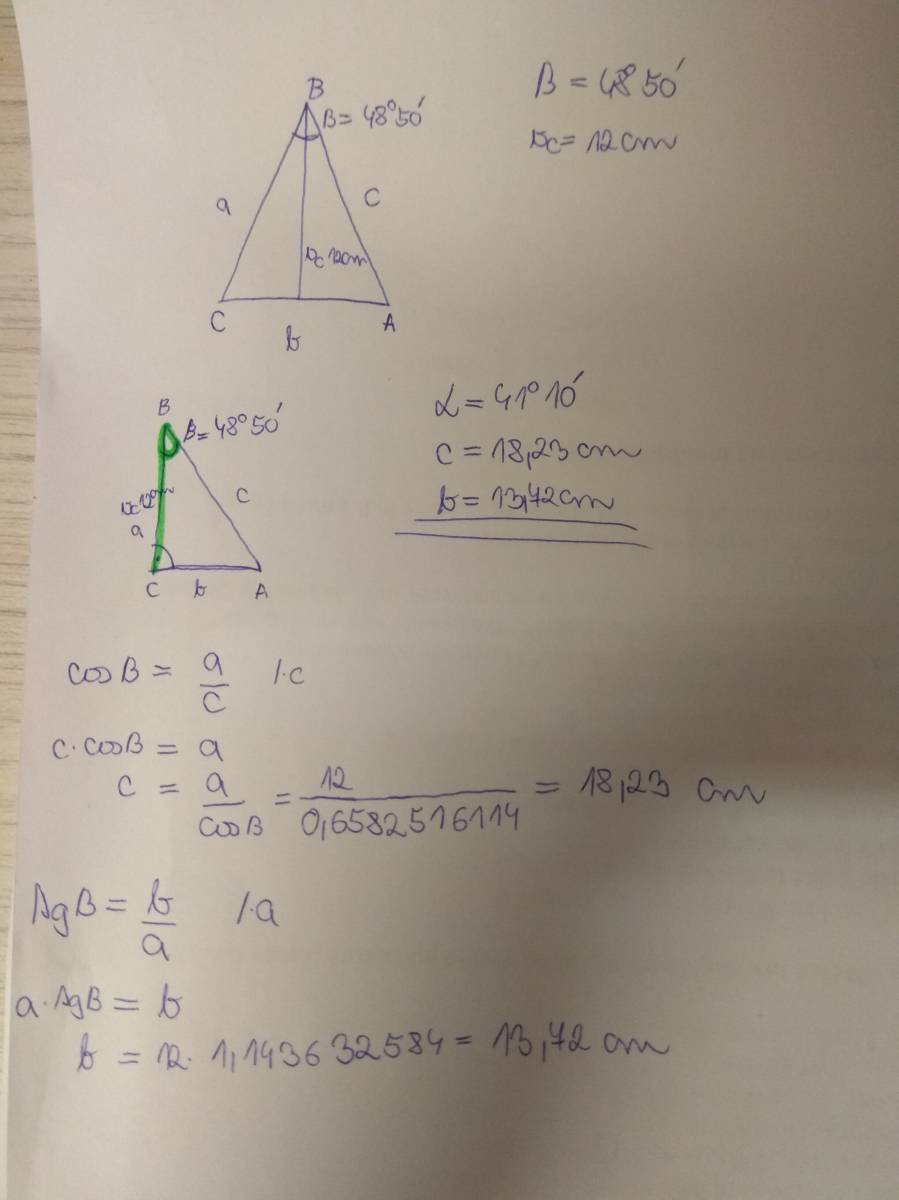
Při výpočtu velikosti neznámého úhlu v trojúhelníku využíváme základní vlastnosti, že součet vnitřních úhlu v trojúhelníku je 180°. Speciální případy: V rovnostranném trojúhelníku mají všechny vnitřní úhly velikost 60°. V rovnoramenném trojúhelníku jsou oba úhly u základny stejné.
Jak zjistit (bez rýsování), jestli je trojúhelník pravoúhlý Jestliže v trojúhelníku platí, že součet druhých mocnin délek dvou kratších stran je roven druhé mocnině délky nejdelší strany, potom je tento trojúhelník pravoúhlý.
Co je to přepona a Odvěsna : Nejdelší strana v pravoúhlém trojúhelníku se nazývá přepona. Přepona leží proti pravému úhlu. Zbývající dvě strany nazýváme odvěsny. Odvěsny svírají pravý úhel.
Jak se měří obsah : Obsah je fyzikální veličina, která vyjadřuje plochu nějakého geometrického tvaru. Obsah se zpravidla měří v čtverečných jednotkách, například čtverečných metrech (m²) nebo čtverečných centimetrech (cm²). Kde π (pi) je matematická konstanta přibližně rovna 3,14159.
Jaký je vzorec pro obvod trojúhelníku
Obvod: mix
| Útvar | Vlastnosti | Obvod |
|---|---|---|
| trojúhelník | strany a , b , c a, b, c a,b,c | o = a + b + c o = a + b + c o=a+b+c |
| čtverec | strana a | o = 4 a o = 4a o=4a |
| obdélník | strany a , b a, b a,b | o = 2 ( a + b ) o = 2(a+b) o=2(a+b) |
| rovnoběžník | strany a , b a, b a,b | o = 2 ( a + b ) o = 2(a+b) o=2(a+b) |
Jak zjistit (bez rýsování), jestli je trojúhelník pravoúhlý Jestliže v trojúhelníku platí, že součet druhých mocnin délek dvou kratších stran je roven druhé mocnině délky nejdelší strany, potom je tento trojúhelník pravoúhlý.Metapontum Village, ItáliePythagoras / Úmrtí
Co vymyslel Pythagoras : V tomto ohledu Pythagoras první použil matematiku ve službách fyziky! Do obecného povědomí vešla především tzv. Pythagorova věta o „součtech čtverců“ stran v pravoúhlém trojúhelníku. Ono c2 = a2 + b2 zná bez nadsázky téměř každý.