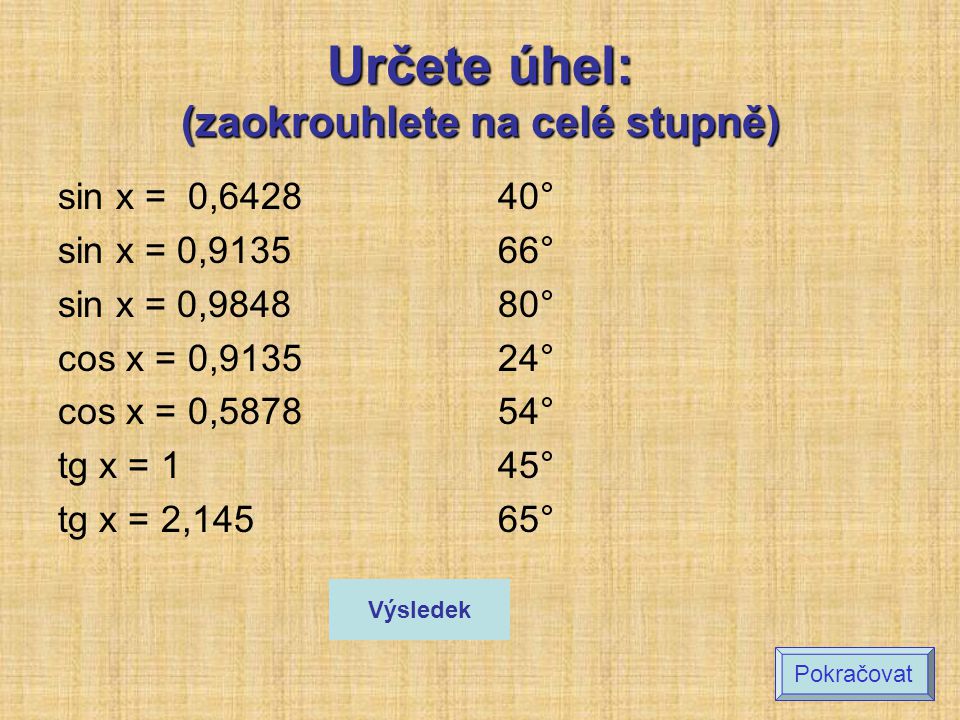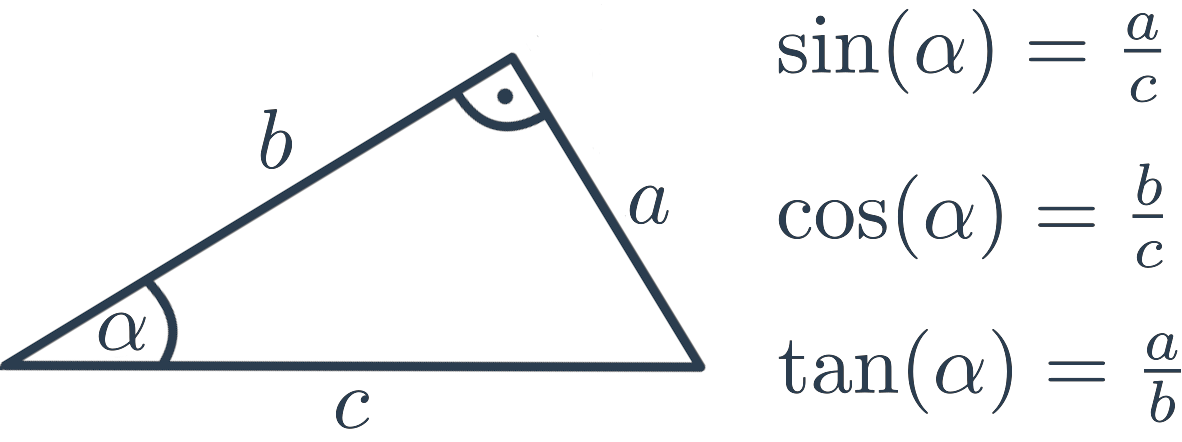
Funkce kosinus
- Funkce kosinus je definována v pravoúhlém trojúhelníku jako poměr přilehlé odvěsny a přepony.
- Jejím grafem je kosinusoida.
- Funkce je definována od −∞ do +∞ a nabývá hodnot od −1 do 1.
Existují ještě dvě další goniometrické funkce, tangens a kotangens. Hlavní rozdíl oproti předchozím goniometrickým funkcím je ten, že tangens a kotangens pracuje pouze s odvěsnami, nepracuje s přeponou. Tangens úhlu α se rovná poměru délky protilehlé odvěsny ku délce přilehlé odvěsny.Goniometrické funkce mají mezi sebou blízké vztahy. Když se podíváte na graf funkce sinus a cosinus současně, tak zjistíte, že se od sebe moc neliší, že jedna je jen trochu posunutá oproti té druhé. A naopak, pokud u cosinu odečteme π/2, dostaneme sinus.
Co je síň cos : Druhou souřadnici bodu jednotkové kružnice na koncovém rameni orientovaného úhlu v základní poloze nazýváme sinus a jeho první souřadnici nazveme kosinus .
Kolik je síň 60
Hodnoty sinus na jednotkové kružnici
| x (úhel) | ||
|---|---|---|
| 60° | π/3 | 1/6 |
| 120° | 2π/3 | 1/3 |
| 75° | 5π/12 | 5/24 |
| 105° | 7π/12 | 7/24 |
Kolik je cos 30 :
| X [º] | X [rad] | cos(x) |
|---|---|---|
| 28 | 0,4887 | 0,8829 |
| 29 | 0,5061 | 0,8746 |
| 30 | 0,5236 | 0,8660 |
| 31 | 0,5411 | 0,8572 |
Sinus a kvadranty
| Stupně | Radiány | sin (x) |
|---|---|---|
| 0° | 0 | 0 |
| 90° | π/2 | 1 |
| 180° | π | 0 |
| 270° | 3π/2 | −1 |
sin(90) = sin(2.035rad) = 0.8939.
Jak se počítá sinus na kalkulačce
Před stiskem samotné klávesy sin, cos nebo tan, je třeba stisknout klávesu, která bývá označena symbolem INV, Shift, 2nd, nebo f–1. Inverzní funkce k sin bývá označována sin–1 nebo arcsin. Inverzní funkce ke cos se značí cos–1 nebo arccos. Inverzní funkce k tan se označuje tan–1 nebo arctan.
| X [º] | X [rad] | cos(x) |
|---|---|---|
| 1 | 0,0175 | 0,9998 |
| 2 | 0,0349 | 0,9994 |
| 3 | 0,0524 | 0,9986 |
| 4 | 0,0698 | 0,9976 |
Nejprve definujeme sin(0) = 0, cos(0) = 1, sin(π/2) = 1, cos(π/2) = 0.
Sinus je goniometrická funkce nějakého úhlu. Zapisuje se jako sin θ, kde θ je velikost úhlu. Pro ostré úhly je definována v pravoúhlém trojúhelníku jako poměr protilehlé odvěsny a přepony (nejdelší strany). Definici lze konzistentně rozšířit jak na všechna reálná čísla, tak i do oboru komplexních čísel.
Kolik je síň 120 : Hodnoty sinus na jednotkové kružnici
| x (úhel) | ||
|---|---|---|
| 45° | π/4 | 1/8 |
| 135° | 3π/4 | 3/8 |
| 60° | π/3 | 1/6 |
| 120° | 2π/3 | 1/3 |
Kolik je síň 90 : sin(90) = sin(2.035rad) = 0.8939.
Kolik je sinus 75
Hodnoty sinus na jednotkové kružnici
| x (úhel) | ||
|---|---|---|
| 135° | 3π/4 | 3/8 |
| 60° | π/3 | 1/6 |
| 120° | 2π/3 | 1/3 |
| 75° | 5π/12 | 5/24 |
| X [º] | X [rad] | sin(x) |
|---|---|---|
| 23 | 0,4014 | 0,3907 |
| 24 | 0,4189 | 0,4067 |
| 25 | 0,4363 | 0,4226 |
| 26 | 0,4538 | 0,4384 |
Nejprve definujeme sin(0) = 0, cos(0) = 1, sin(π/2) = 1, cos(π/2) = 0.
Co to je síně : Šína je obroučka, kroužek.
(Zároveň je šína pojem, který se používá hned v několika branžích, tak se nenechte zmást.)