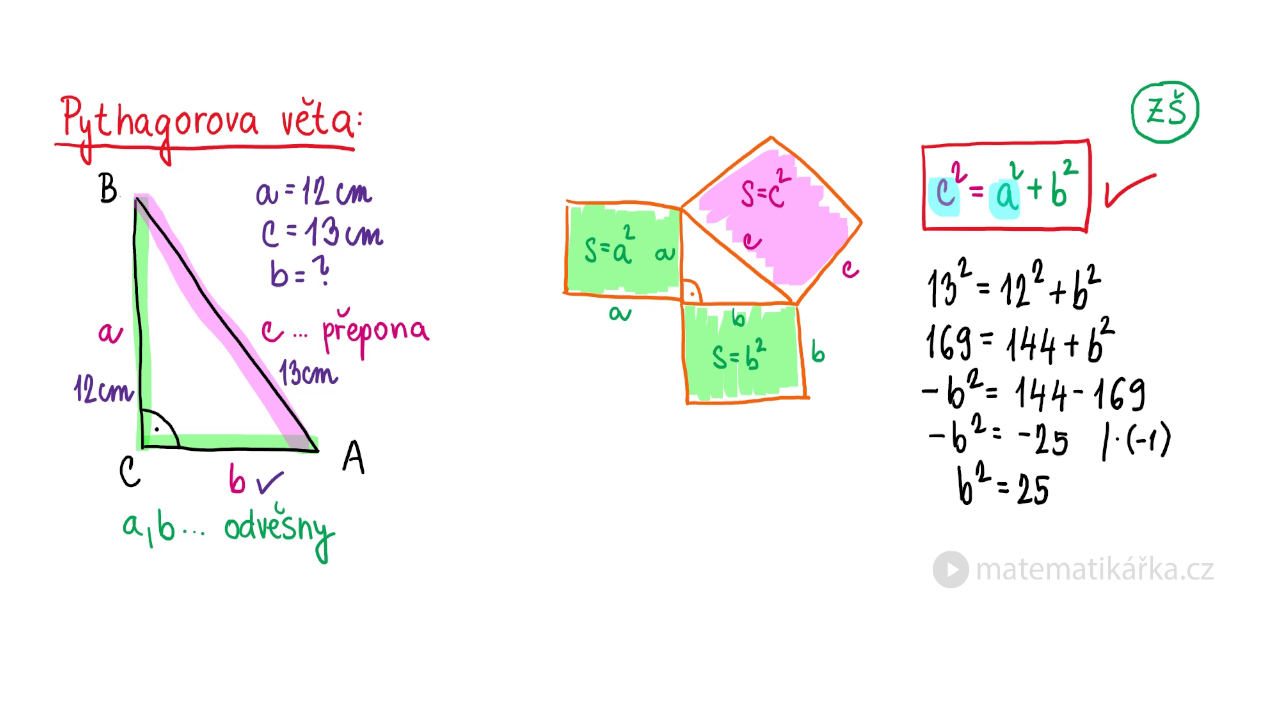
Přepona pravoúhlého trojúhelníku je vždy ta strana, která se nachází naproti pravému úhlu. Tato strana je v trojúhelníku nejdelší. Další dvě strany jsou nazvány protilehlá a přilehlá odvěsna. Jsou takto nazvány vzhledem k danému úhlu.Pythagorova věta: základní použití
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .Nejdelší strana v pravoúhlém trojúhelníku se nazývá přepona. Přepona leží proti pravému úhlu. Zbývající dvě strany nazýváme odvěsny. Odvěsny svírají pravý úhel.
Jak zjistit zda li je trojúhelník Pravouhly : Jak zjistit (bez rýsování), jestli je trojúhelník pravoúhlý Jestliže v trojúhelníku platí, že součet druhých mocnin délek dvou kratších stran je roven druhé mocnině délky nejdelší strany, potom je tento trojúhelník pravoúhlý.
Co je Prilehla Odvesna
Přilehlá a protilehlá odvěsna se vztahují k úhlu α. je poměr délky odvěsny přilehlé tomuto úhlu a délky přepony.
Jak se značí Odvěsna : Co je vlastně ten pravoúhlý trojúhelník Pravoúhlý trojúhelník je geometrický útvar, jehož 2 strany svírají pravý úhel (= úhel o velikosti 90°). Těmto stranám se říká odvěsny a obecně se značí písmeny a, b.
Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.
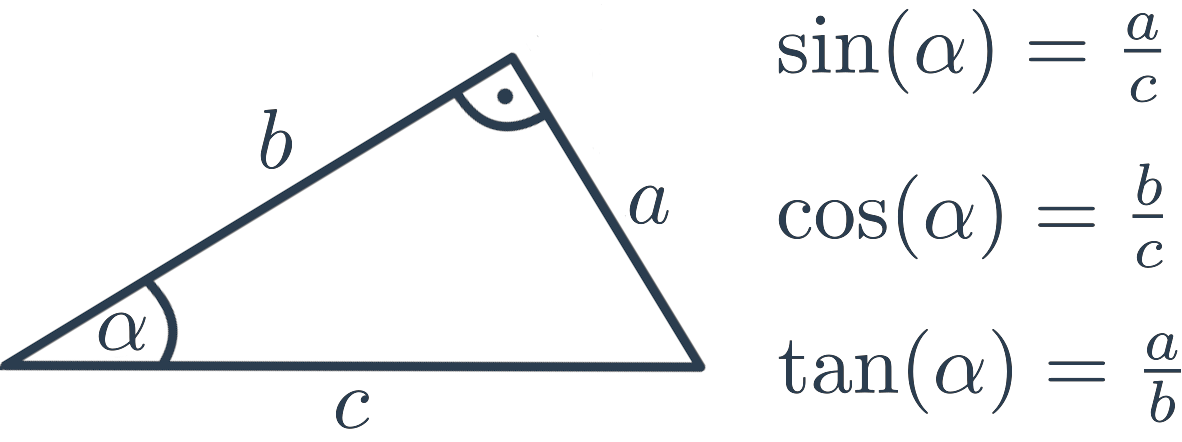
Vzorce: Pythagorovu větu můžeme zapsat vztahem c² = a² + b², kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.
Jak se pozna pravý úhel
Pravý úhel je úhel, který tvoří polovinu přímého úhlu či čtvrtinu plného úhlu. Jeho numerická hodnota ve stupních je 90, v radiánech π/2. Název pravý úhel vznikl nepřesným překladem latinského termínu angulus rectus, kde ovšem slovo rectus bylo původně použito ve významu „vzpřímený“, nikoli „pravý“.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .Pravoúhlý trojúhelník má jeden vnitřní úhel o velikosti 90 stupňů. Oba zbývající vnitřní úhly musí mít nutně velikost menší než 90 stupňů, aby součet vnitřních úhlů byl roven 180 stupňů. Součet dvou zbývajících úhlů je tedy právě 90 stupňů.
Goniometrické funkce a pravoúhlý trojúhelník
- Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony.
- Kosinus ( cos) úhlu α je poměr délky odvěsny přilehlé úhlu α a délky přepony.
- Tangens ( tan) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky odvěsny přilehlé úhlu α.
Co je základna u trojúhelníku : Strana, která není shodná s rameny, se nazývá základna. Vrchol naproti základně se nazývá hlavní vrchol.
Co je to Odvesna : Odvěsna je v geometrii součástí pravoúhlého trojúhelníka. Jako odvěsny jsou označovány jeho dvě kratší strany svírající pravý úhel. Protilehlá nejdelší strana se nazývá přepona.
Co je přepona u trojúhelníku
Pravoúhlý trojúhelník má tři strany, dvěma z nich se říká odvěsny (modré strany), a třetí strana se nazývá přepona (červená strana) – to je ta nejdelší strana.
Střední příčka trojúhelníku je úsečka, jejímiž krajními body jsou středy stran tohoto trojúhelníku. Vlastnosti: 1. Střední příčka je rovnoběžná se stranou, jejímž středem neprochází.Jak změřit pravý úhel metrem
Když si za pomoci kolíků a provázku sestrojíte trojúhelník o poměru stran 3 : 4 : 5, úhel proti přeponě bude vždy pravý. Tak vám k měření pravého úhlu stačí pouze metr. Jen si dejte pozor, ať poměr stran skutečně sedí, i když provázek navážete na kolíky.
Jak vypadá přímý úhel : Přímé úhly
Přímý úhel vypadá jako rovná přímka. Příklad přímého úhlu můžeš vidět na obrázku dole.




