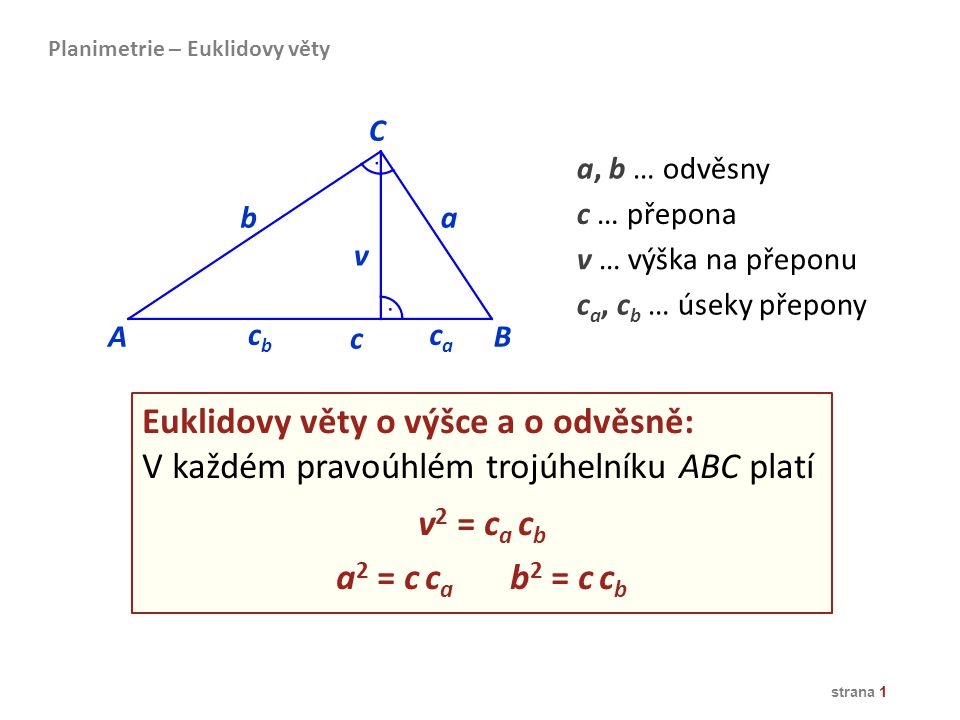
V pravoúhlém trojúhelníku je přepona nejdelší stranou. "Protilehlá odvěsna" je strana naproti zadanému úhlu a "přilehlá odvěsna" je strana vedle daného úhlu. Pro popsání stran pravoúhlého trojúhelníku používáme speciální terminologii.Přilehlá a protilehlá odvěsna se vztahují k úhlu α. je poměr délky odvěsny přilehlé tomuto úhlu a délky přepony.Pythagorova věta popisuje vztah, který platí mezi délkami stran pravoúhlého trojúhelníku. Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami.
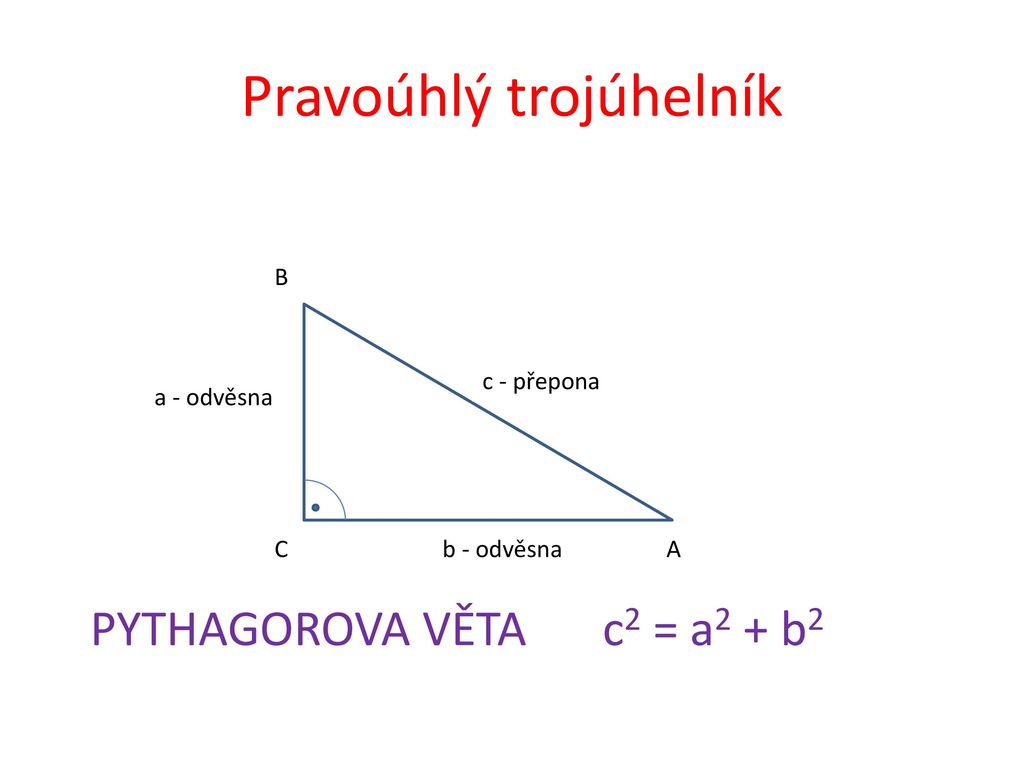
Jak se značí Odvěsna : Co je vlastně ten pravoúhlý trojúhelník Pravoúhlý trojúhelník je geometrický útvar, jehož 2 strany svírají pravý úhel (= úhel o velikosti 90°). Těmto stranám se říká odvěsny a obecně se značí písmeny a, b.
Jak Dopocitat Odvesnu
Pythagorova věta
- c2 = a2 + b2 – tedy:
- Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených nad jeho odvěsnami.
Jak se pozna pravý úhel : Pravý úhel je úhel, který tvoří polovinu přímého úhlu či čtvrtinu plného úhlu. Jeho numerická hodnota ve stupních je 90, v radiánech π/2. Název pravý úhel vznikl nepřesným překladem latinského termínu angulus rectus, kde ovšem slovo rectus bylo původně použito ve významu „vzpřímený“, nikoli „pravý“.
Goniometrické funkce můžeme v pravoúhlém trojúhelníku vyjádřit následovně: Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony.
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Jak zjistit zda li je trojúhelník pravoúhlý
Jak zjistit (bez rýsování), jestli je trojúhelník pravoúhlý Jestliže v trojúhelníku platí, že součet druhých mocnin délek dvou kratších stran je roven druhé mocnině délky nejdelší strany, potom je tento trojúhelník pravoúhlý.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .Nejdelší strana v pravoúhlém trojúhelníku se nazývá přepona. Přepona leží proti pravému úhlu. Zbývající dvě strany nazýváme odvěsny. Odvěsny svírají pravý úhel.
Pravoúhlý trojúhelník má samozřejmě tři strany, dvěma z nich se říká odvěsny (červené strany), to jsou ty menší strany a třetí strana se nazývá přepona (modrá strana) — to je ta nejdelší strana. Přepona je vždy naproti bodu, u kterého je pravý úhel.
Jak změřit pravý úhel na strese : Jak změřit pravý úhel metrem
Když si za pomoci kolíků a provázku sestrojíte trojúhelník o poměru stran 3 : 4 : 5, úhel proti přeponě bude vždy pravý. Tak vám k měření pravého úhlu stačí pouze metr. Jen si dejte pozor, ať poměr stran skutečně sedí, i když provázek navážete na kolíky.
Jak poznam Tupy úhel : Pravé úhly měří 90 stupňů. Tupé úhly měří více než 90 stupňů.
Jak si zapamatovat sinus
Sinová věta: Řekni, milý Jakube, čemu rovno a ku b; sinová to praví věta: sinus alfa ku sinus beta. Prvních šest číslic odmocniny ze dvou – 1.41421 – Čtrnáct dní, čtrnáct dní, tři neděle.
sin(90) = sin(2.035rad) = 0.8939.Goniometrické funkce a pravoúhlý trojúhelník
- Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony.
- Kosinus ( cos) úhlu α je poměr délky odvěsny přilehlé úhlu α a délky přepony.
- Tangens ( tan) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky odvěsny přilehlé úhlu α.
Co platí pro pravoúhlý trojúhelník : Pravoúhlý trojúhelník má jeden vnitřní úhel o velikosti 90 stupňů. Oba zbývající vnitřní úhly musí mít nutně velikost menší než 90 stupňů, aby součet vnitřních úhlů byl roven 180 stupňů. Součet dvou zbývajících úhlů je tedy právě 90 stupňů.