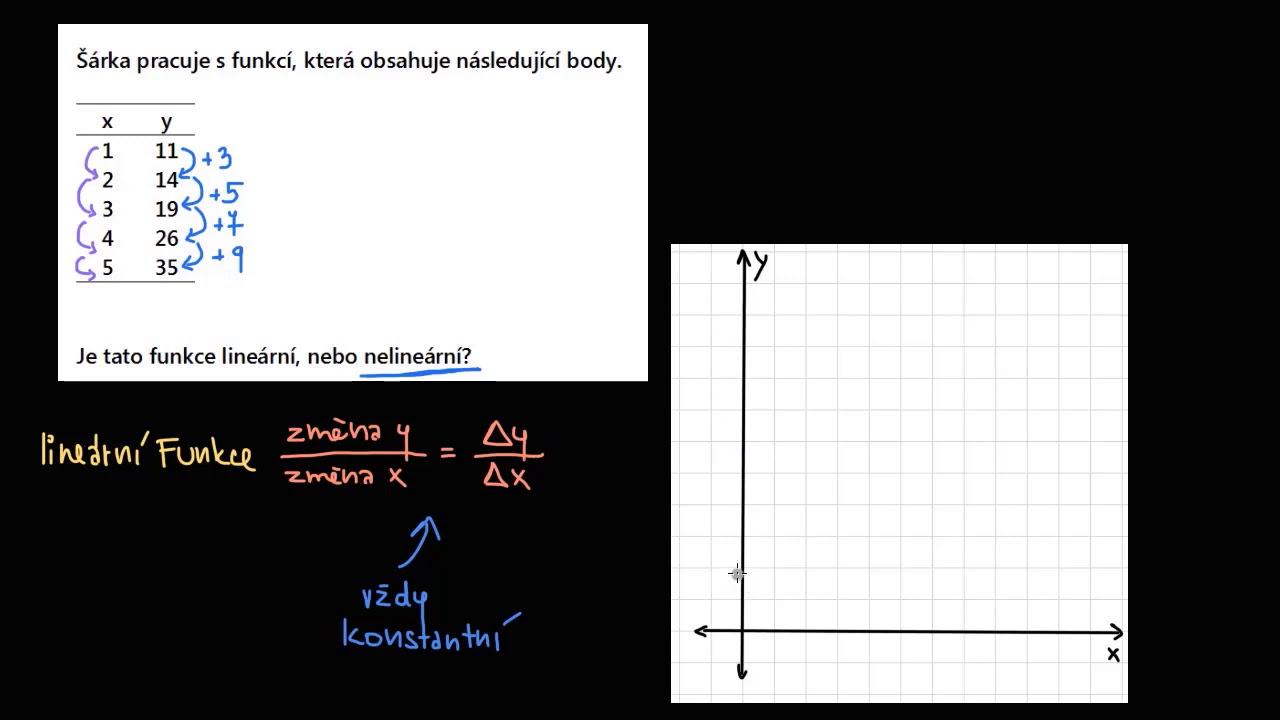
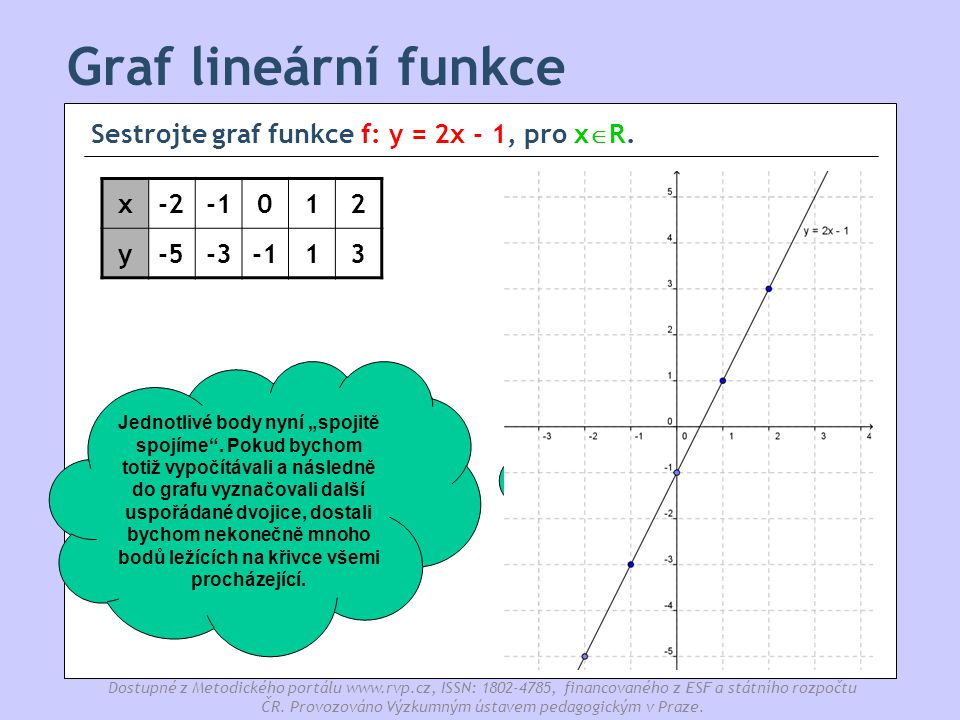
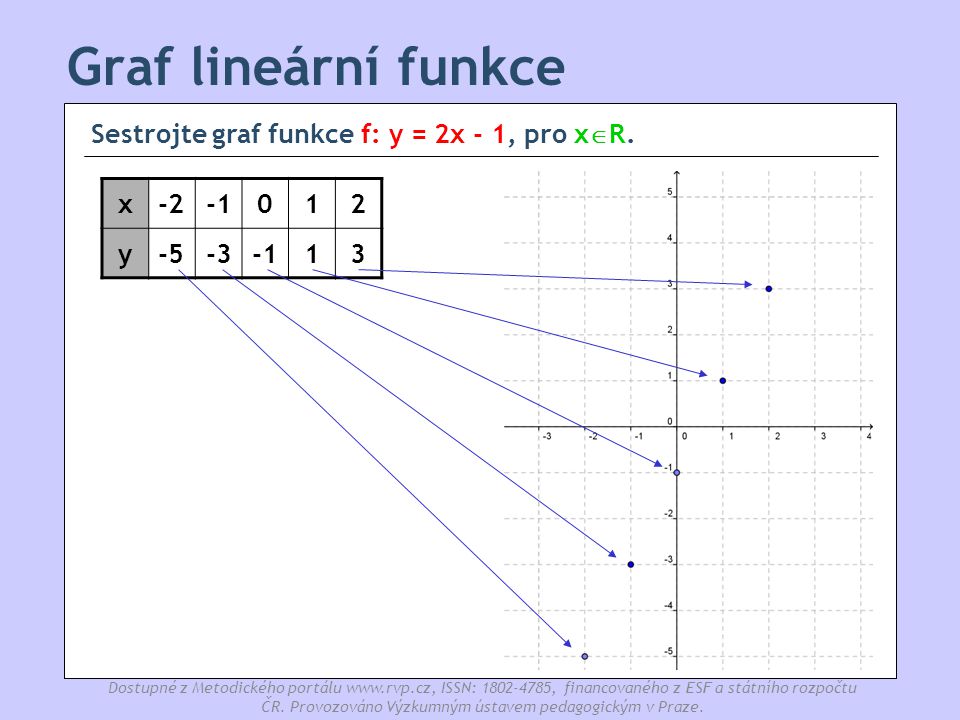
U lineární funkce, když máme nějakou změnu x, která je stejná, když se nám x mění o nějakou stejnou hodnotu, tak se nám i y musí měnit o stejnou hodnotu, ta změna musí být konstantní. Pokud se při změně x mění y o stále stejnou hodnotu, pak se jedná o lineární funkci.Co to vlastně znamená 'lineární' Toto slovo pochází z latinského linea, což označuje čáru nebo přímku. Grafem lineární funkce tedy bude přímka. Předpis lineární funkce je f:y=ax+b.Slovo 'lomené' nám napovídá, že v předpisu funkce bude zlomek. Lineární lomená funkce je podíl dvou lineárních funkcí. f:y=\frac{ax+b}{cx+d}, kde a, b, c, d jsou reálná čísla, c \ne 0 a ad-bc \ne 0.
Jak poznat konstantní funkci : V matematice se pojmem konstantní funkce označuje taková funkce, jejíž funkční hodnota je v celém definičním oboru stejná, tedy konstantní. Například funkce f(x) = 4 je konstantní.
Jak vypadá lineární rovnice
Základní tvar lineární rovnice vypadá takto: a x + b = 0 , kde x je neznámá a symboly a a b jsou libovolná reálná čísla.
Co je to lineární : Slovo lineární pochází z latinského linearis, co znamená tvořeno přímkami. Obvykle slovo označuje podobnost něčeho s přímkou nebo rovností. Specifická použití tohoto výrazu jsou například: V matematice.
Termín lineární rovnice v matematice označuje algebraickou rovnici prvního stupně, tzn. rovnici o jedné neznámé, ve které neznámá vystupuje pouze v první mocnině.
Funkce – úvod, typy
- Racionální funkce je každá funkce daná ve tvaru:
- Polynomická funkce je každá funkce ve tvaru.
- funkce konstantní:
- lineární funkce:
- funkce s absolutní hodnotou:
- kvadratická funkce:
- mocninné funkce s přirozeným exponentem:
Jak zjistit inverzní funkci
Ke každé prosté funkci f existuje funkce k ní inverzní, kterou značíme f−1. Inverzní funkce f−1 je definována následujícím vztahem: y=f(x)⇔x=f−1(y). Vztah funkce f a funkce k ní inverzní f−1 si lze představit také tak, že si proměnné x a y vymění roli.Lineární rovnice je taková rovnice, kterou můžeme upravit na tvar ax + b = 0, kde a≠0.Řešíme-li lineární rovnici ax + b = 0, kde a, b ∈ R , nastane právě jedna z možností: a) a = 0 , rovnice má jedno řešení x = − b a ; b) a = 0, b = 0 , řešením rovnice jsou všechna x ∈ R ; c) a = 0, b = 0 , rovnice nemá řešení.
Linearita. Linearita je ukazatelem vlastnosti měřicího systému. Její hodnota představuje maximální hodnotu chyby mezi ideální hodnotou a skutečným výsledkem měření. Pokud se například objekt posune o 1 mm pomocí měřícího systému s linearitou ±5 µm, říkáme, že zobrazená hodnota může zahrnovat chybové rozpětí ±5 µm (např …
Jak vysvětlit lineární rovnice :
- Lineární rovnice poznáme jednoduše podle toho, že veškeré výrazy s neznámou ji mají pouze v první mocnině.
- Základní strategie je vždy dostat s výrazy s neznámou na jednu stranu a čísla na stranu druhou a pak na straně s neznámou získat pouze jedno x.
Co to je lineární : Slovo lineární pochází z latinského linearis, co znamená tvořeno přímkami. Obvykle slovo označuje podobnost něčeho s přímkou nebo rovností. Specifická použití tohoto výrazu jsou například: V matematice.
Co znamená f x
Značení y = f (x) znamená, že k hodnotě argumentu x přiřazuje funkce f hodnotu y. Někdy se také používá značení f : x ↦ y, slovy, funkce f posílá x na y. Nejobvyklejší způsob, jak zadat toto přiřazování, je pomocí nějakého vzorce, tj.
Obvykle ji značíme y nebo f(x). Jiný název pro argument funkce. Nezávislost je dána tím, že její hodnotu můžeme libovolně měnit (v rámci množiny D). Takto také nazýváme funkční hodnotu.Funkce
- Funkci nazveme rostoucí tehdy, když s rostoucí hodnotou x roste hodnota y.
- Funkce je klesající tehdy, když s rostoucí hodnotou x klesá hodnota y.
- Funkci nazveme nerostoucí tehdy, když s rostoucí hodnotou x klesá nebo se nemění hodnota y.
Jak poznat Prostost funkce : Funkce f se nazývá prostá, pokud se žádné dvě různé hodnoty proměnné x nezobrazí na tutéž hodnotu f(x). Ekvivalentně, pokud má každý prvek z oboru hodnot pouze jeden vzor. Matematicky zapsáno, funkce f je prostá právě když pro každé x1,x2∈D(f) platí následující: Je-li x1≠x2, je také f(x1)≠f(x2).