
Předpis lineární funkce je f:y=ax+b. Pomocí koeficientů a a b můžeme ovlivnit vzhled grafu lineární funkce, jestli bude funkce rostoucí, nebo klesající a kde graf protne osu y. f:y=ax+b, kde a a b jsou reálná čísla.Kvadratická funkce je taková funkce, kterou lze vyjádřit předpisem f(x) = ax2 + bx + c, kde a, b, c jsou reálná čísla a dále a ≠ 0. Stejně jako lineární funkce je vždy popsána přímkou, kvadratická funkce je zase vždy popsána parabolou.U lineární funkce, když máme nějakou změnu x, která je stejná, když se nám x mění o nějakou stejnou hodnotu, tak se nám i y musí měnit o stejnou hodnotu, ta změna musí být konstantní. Pokud se při změně x mění y o stále stejnou hodnotu, pak se jedná o lineární funkci.
Jaké jsou typy funkci : Funkce – úvod, typy
- Racionální funkce je každá funkce daná ve tvaru:
- Polynomická funkce je každá funkce ve tvaru.
- funkce konstantní:
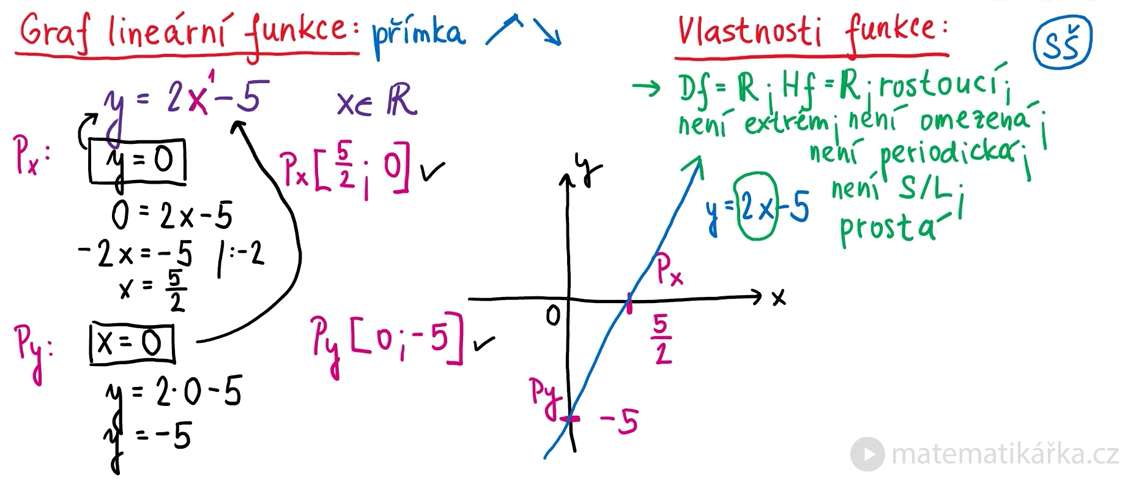
- lineární funkce:
- funkce s absolutní hodnotou:
- kvadratická funkce:
- mocninné funkce s přirozeným exponentem:
Co je to předpis funkce
Funkční předpis je pravidlo (formulované slovně nebo častěji pomocí matematických symbolů), podle kterého je ke každému číslu x ∈ D(f) přiřazena jednoznačně funkční hodnota y= f(x). Analytické zadání – funkční předpis je dán vzorcem, tj. rovnicí tvaru y=f(x), např. f(x)=2x-5, y=3x+3.
Jak najít předpis inverzní funkce : Předpis inverzní funkci najdeme tak, že z předpisu y=f(x) osamostatníme x a zapíšeme ho jako funkci proměnné y. Výměnou symbolů x a y získáme předpis inverzní funkce y=f−1(x). Definiční obor inverzní funkce f−1 určíme jako D(f−1)=H(f).
Funkce, jejíž funkční hodnota se mění úměrně druhé mocnině nezávisle proměnné, je příkladem kvadratické funkce. Grafu kvadratické funkce se říká parabola. Graf je symetrický podle osy paraboly, tato osa je rovnoběžná s osou y.
Jak zjistíme vrchol paraboly Souřadnice vrcholu paraboly jednoduše zjistíme díky vzorečku -b/2a. Na základě tohoto vzorce zjistíme x-ovou souřadnici vrcholu a y-ovou spočítáme pouhým dosazením do předpisu funkce.
Jak se počítají lineární funkce
Lineární funkce je dána předpisem y = ax + b (a a b jsou reálná čísla). Grafem je přímka, která prochází body o souřadnicích [0; b], [1; a + b]. Pokud je a > 0 – funkce je rostoucí. Pokud je a < 0 – funkce je klesající.Lineární lomená funkce je každá funkce daná předpisem f(x)=ax+bcx+d,c≠0, cb−ad≠0. Výraz ax+bcx+d má smysl, když cx+d≠0, nulou nelze dělit. Definičním oborem jsou všechna reálná čísla kromě −dc, tj. D(f)=R∖{−dc}.Značení y = f (x) znamená, že k hodnotě argumentu x přiřazuje funkce f hodnotu y. Někdy se také používá značení f : x ↦ y, slovy, funkce f posílá x na y. Nejobvyklejší způsob, jak zadat toto přiřazování, je pomocí nějakého vzorce, tj.
Obvykle ji značíme y nebo f(x). Jiný název pro argument funkce. Nezávislost je dána tím, že její hodnotu můžeme libovolně měnit (v rámci množiny D). Takto také nazýváme funkční hodnotu.
Jak se počítá inverzní funkce : Z definice funkce platí, že pro všechny prvky x z definičního oboru D(f) máme nějaký prvek y z oboru hodnot H(f), pro který platí f(x) = y. Inverzní funkce f−1 je pak funkce, pro kterou platí: f ( x ) = y ⇔ f − 1 ( y ) = x .
Co to je inverzní funkce : Inverzní funkce k nějaké funkci je funkce, která funguje přesně "obráceně" než původní funkce.
Co je to kvadratická funkce jaký je její předpis co je grafem funkce
Funkce je kvadratická, pokud ji lze vyjádřit ve tvaru f ( x ) = a x 2 + b x + c f(x) = ax^2 + bx + c f(x)=ax2+bx+c, kde a ≠ 0 a\neq 0 a=0. Funkce je ryze kvadratická, pokud nemá lineární člen (tj. b = 0 b=0 b=0). Grafem kvadratické funkce je parabola.
Značení y = f (x) znamená, že k hodnotě argumentu x přiřazuje funkce f hodnotu y. Někdy se také používá značení f : x ↦ y, slovy, funkce f posílá x na y. Nejobvyklejší způsob, jak zadat toto přiřazování, je pomocí nějakého vzorce, tj.Asi nejjednodušší je použít vzorec pro výpočet souřadnic vrcholu. Vzorec říká, že x-ová souřadnice vrcholu je minus b lomeno dvě a, kdy a je parametr u x na druhou a b je parametr u x.
Jaké jsou druhy grafu : Nejběžnějšími typy grafů jsou čárové grafy, sloupcové grafy, svíčkové grafy, bodové grafy a číselné grafy. Ne každý typ grafu je však vhodný pro každý typ finančního nástroje. Například opce na různá podkladová aktiva mají často velmi nízký objem obchodování a v některých dnech se s nimi dokonce neobchoduje.






