Shodnost úseček je vztah mezi úsečkami, který je v geometrii zaveden pomocí axiomů shodnosti. Je to relace reflexivní, symetrická a tranzitivní na množině všech úseček v prostoru, tedy ekvivalence, která rozkládá množinu všech úseček na třídy navzájem shodných úseček.Dvě přímky p(P, u) a q(Q, v) jsou totožné právě tehdy, jsou-li rovnoběžné a leží-li bod Q na přímce p. Jsou-li přímky p(P, u) a q(Q, v) totožné, pak jsou rovnoběžné (u je násobkem v) a bod Q leží na přímce p.Úsečka – je část přímky, ohraničená dvěma krajními body. Úsečku označujeme krajními body, takže můžeme mluvit o úsečce AB, pokud má krajní body A a B.
Co je střed úsečky : Střed úsečky je bod, který leží na úsečce a jehož vzdálenost od obou krajních bodů je stejná. Osa úsečky je přímka kolmá k úsečce procházející jejím středem. Všechny body na ose úsečky mají od obou krajních bodů stejnou vzdálenost. Úsečka je středově souměrná podle svého středu.
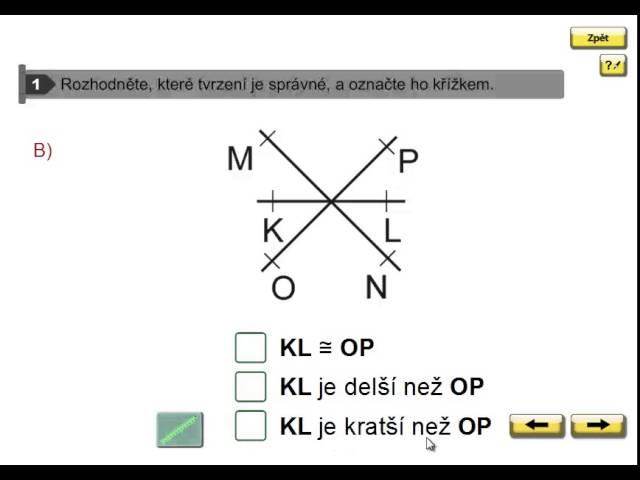
Kdy jsou úsečky shodné
Shodné úsečky mají stejnou délku.
Co to je shodnost : Shodné zobrazení je v geometrii takové zobrazení mezi Euklidovskými prostory, které zachovává vzdálenost. Shodné zobrazení prostoru do sebe se nazývá shodnost. V elementární školské geometrii se studují shodnosti v rovině a (trojrozměrném) prostoru.
sss, sus, uu Označení věty zkratkou vyjadřuje, kterými údaji trojúhelníky porovnáváme. VĚTA sss Každé dva trojúhelníky, které mají sobě rovné poměry délek všech tří dvojic odpovídajících si stran, jsou podobné.
Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí. Co nám tedy na obrázku vyznačuje šipka Lze tedy polopřímku změřit ÚSEČKA je rovná čára, která má dva krajní body (značíme velkými tiskacími písmeny
Jak zjistit střed úsečky
Způsobů je několik, ale nejklasičtější je protnutí dvou kružnic se stejným poloměrem, větším než je polovina úsečky, a se středy na koncích úsečky. Spojnice těchto průsečíků je k přímce kolmá a půlí ji (prochází středem).1. Jak sestrojíme střed úsečky
- Úsečka AB.
- Dva oblouky kružnice z bodu A.
- Dva stejně velké oblouky(stejné poloměry jako oblouky z bodu A) z bodu B → vzniknou body X a Y.
- Spojnice bodů X a Y rozdělí úsečku na 2 poloviny a vznikne tak střed S.
Shodná zobrazení Zobrazení f v rovině je shodné zobrazení, jestliže pro každé dva body X, Y roviny a jejich obrazy X', Y' platí |XY|=|X'Y'|. Shodné zobrazení v rovině se rovněž nazývá shodnost. Z definice shodného zobrazení plyne, že každé shodné zobrazení je prosté.
Přímá a nepřímá shodnost
Shodnost zachovávající orientaci se nazývá přímá neboli přemístění. Shodnost měnící orientaci se nazývá nepřímá. Posunutí a otočení (a tedy i středová souměrnost) jsou přímé shodnosti (přemístění), zachovávají orientaci. (Posunuté) osové souměrnosti jsou nepřímé shodnosti, mění orientaci.
Co je prima shodnost : Přímá shodnost je každá shodnost, ve které jsou libovolný trojúhelník a jeho obraz přímo shodné.
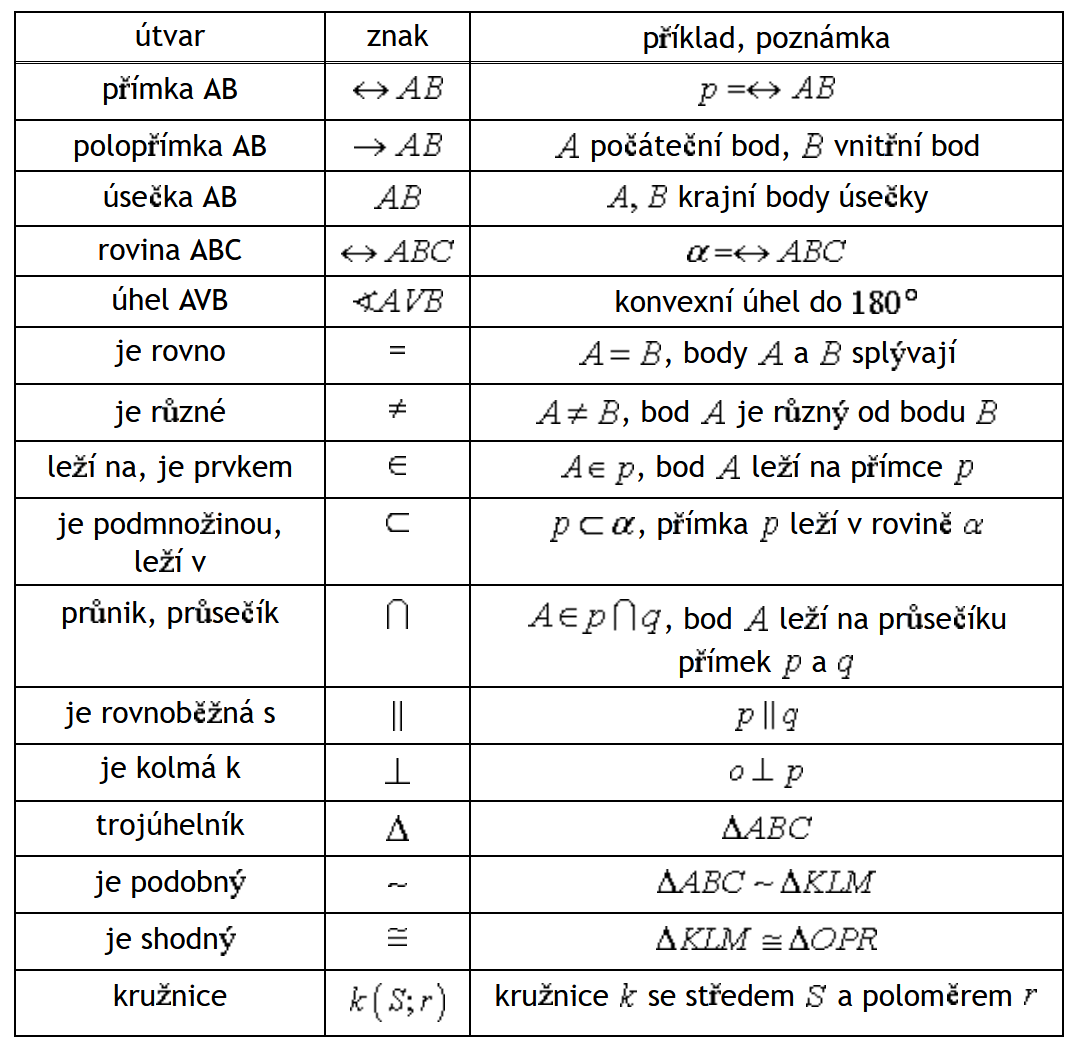
Jak se zapisuje shodnost : Stručně se označují sss, sus, usu, Ssu, přičemž věta sss je vlastně definicí 1.3.
Co je to výška trojúhelníku
Výška trojúhelníku je kolmá úsečka spuštěná z vrcholu na přímku procházející protější stranou. Průsečík výšky s touto přímkou se nazývá pata výšky. Každý trojúhelník má tři výšky. Menší straně odpovídá větší výška.
Rovina je v matematice dvourozměrný geometrický útvar, který si lze představit jako neomezenou dokonale rovnou plochu. Algebraicky vyjádřeno, jde o množinu bodů izomorfní s dvoudimenzionálním lineárním prostorem. Jinak řečeno jde o dvoudimenzionální afinní prostor.Vzdálenost bodů A [xA], B [xB] na číselné ose je rovna absolutní hodnotě rozdílu reálných čísel xA a xB . Vzdálenost |AB| dvou bodů A [xA ; yA ; zA ], B [xB ; yB ; zB] v prostoru je dán vzorcem: Vzdálenost dvou bodů A, B je rovna velikosti ( délce ) úsečky AB.
Jak změřit střed kruhu : Označte střed tečkou nebo křížkem. To bude váš výchozí bod. Nakreslete dvě čáry od této tečky na obě strany kruhu, jednu čáru rovnoběžnou s horním a dolním okrajem a jednu čáru rovnoběžnou s levým a pravým okrajem. V místě, kde se tyto dvě čáry protínají, najdete středový bod.