Variační koeficient (The Coefficient of Variation)
Variační koeficient je vhodný pro vzájemné srovnávání variability dvou nebo více souborů s podstatně odlišnou úrovní hodnot (např. variabilitu váhy kuřat v gramech a variabilitu váhy skotu v kg nebo metrických centech).Rozptyl bodů nám pak říká, jaké jsou mezi jednotlivými studenty rozdíly. Pokud je rozptyl velký, znamená to, že jednotliví studenti se vzájemně velmi liší svými vědomostmi. Čím je rozptyl nižší, tím jsou si jednotliví studenti svými výkony bližší. Ukazatelů variability existuje více.Ukazuje, jak jsou hodnoty proměnné rozptýleny kolem průměru. Malá směrodatná odchylka nám říká, že hodnoty proměnné jsou koncentrovány kolem průměru. Pro snazší porovnání toho, jak velká je směrodatná odchylka v různých souborech vzhledem k průměru, slouží variační koeficient.

Jak se vypočítá Variační koeficient v Excelu : V Excelu využijeme tyto funkce:
- PRŮMĚR pro aritmetický průměr (v angl. AVERAGE)
- GEOMEAN pro geometrický průměr.
- variační rozpětí nemá vlastní funkci, spočteme jako rozdíl =MAX(D9:D21)-MIN(D9:D21)
- MIN pro minimum, MAX pro maximum.
Co znamená R ve statistice
(„R kvadrát“), je v matematické statistice míra kvality regresního modelu, která ve své základní podobě vyjadřuje, jaký podíl variability závisle proměnné model vysvětluje.
Co mi říká rozptyl : Rozptyl je definován jako průměrná kvadratická odchylka mezi údaji souboru a jejich aritmetickým průměrem. Podle Hendla není při větších rozsazích významný rozdíl mezi číslem n nebo n – 1.
Rozptyl nám udává, jak moc jsou hodnoty v našem statistickém soubory rozptýleny. Rozptylu se někdy též říká variance.
. Směrodatná odchylka vypovídá o tom, nakolik se od sebe navzájem typicky liší jednotlivé případy v souboru zkoumaných hodnot. Je-li malá, jsou si prvky souboru většinou navzájem podobné, a naopak velká směrodatná odchylka signalizuje velké vzájemné odlišnosti.
Co je rozptyl a směrodatná odchylka
Rozptyl a směrodatná odchylka jsou v teorii i praxi nejčastěji používané míry variability analyzovaných veličin. Měří proměnlivost (variabilitu) empirických hodnot okolo jejich střední hodnoty (aritmetického průměru).Koeficient korelace
Korelace ρ(X,Y) měří lineární závislost mezi veličinami X a Y a standardizuje hodnoty kovariance. Počítá se jako poměr kovariance C(X,Y) veličin X a Y k součinu směrodatných odchylek D(X)·D(Y) veličin X a Y.Rozptyl (angl. variance, zkratka s2) je poměrně často užívanou mírou variability. Rovná se průměrnému čtverci odchylky hodnoty ze statistického souboru od aritmetického průměru. Čím je rozptyl větší, tím více se údaje odchylují od průměru.
V matematické statistice je četnost veličina, která udává, kolik hodnot daného znaku se vyskytuje ve statistickém souboru. Jedná se o statistický znak, jenž nabývá hodnot x1, x2, …, xn, kde n je rozsah uvažovaného statistického souboru.
Co je rozptyl ve statistice : Jedná se o charakteristiku variability rozdělení pravděpodobnosti náhodné veličiny, která vyjadřuje variabilitu rozdělení souboru náhodných hodnot kolem její střední hodnoty.
Jak se vypočítá rozptyl : Rozptyl se vypočítá jako průměr čtverců odchylek od průměru. Rozptyl vychází v kvadrátu (mocnině) a proto je těžké si pod jeho hodnotou něco představit. Právě z tohoto důvodu je vhodnější k interpretaci použít směrodatnou odchylku, která se spočítá jako odmocnina z rozptylu.
Co udává koeficient determinace
(„R kvadrát“), je v matematické statistice míra kvality regresního modelu, která ve své základní podobě vyjadřuje, jaký podíl variability závisle proměnné model vysvětluje.
b) Regresní koeficient q určuje průsečík přímky s osou y:
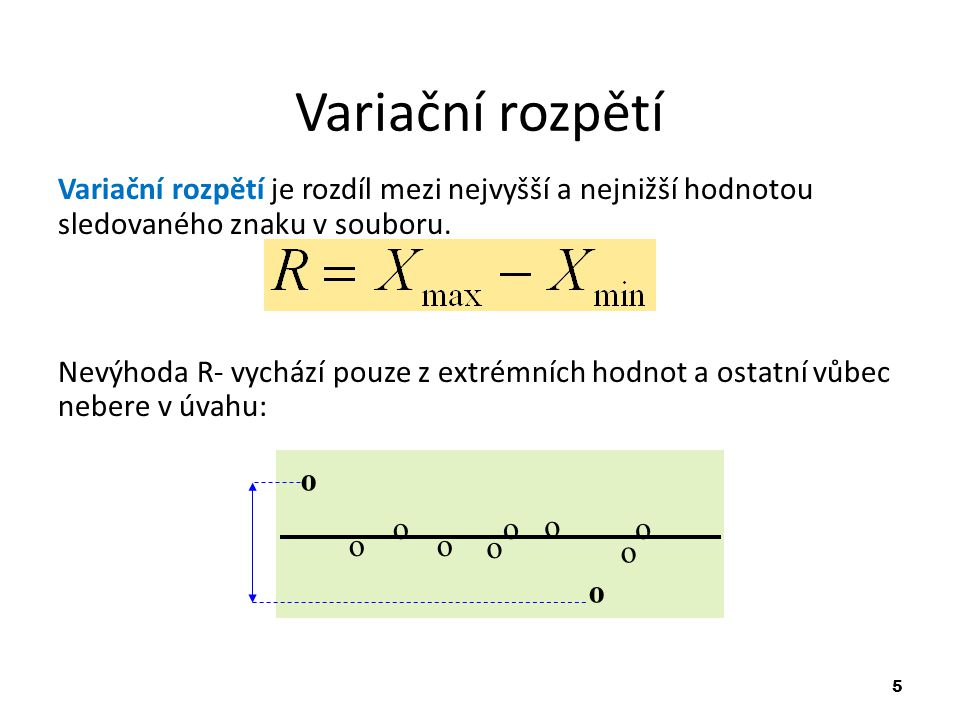
V případě kladné hodnoty koeficientu q protíná přímka osu y nad počátkem souřadnicových os, v případě záporné hodnoty koeficientu q protíná přímka osu y pod počátkem souřadnicových os.Variační šíře (neboli rozpětí) je nejjednodušší mírou variability. Počítá se jako rozdíl největší a nejmenší hodnoty souboru: R = x m a x − x m i n .
Kdy se používá ANOVA : ANOVA se používá tam, kde končí možnosti t-testu. ANOVA použijeme, máme-li více než dva vzorky a více než jednu nezávislou proměnnou. Z důvodu zachování úrovně statistické významnosti není vhodné použít více t-testů a testovat vždy dva vzorky proti sobě.