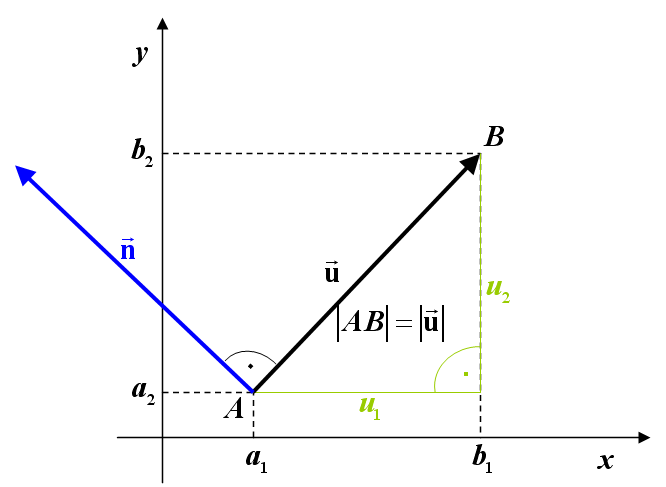
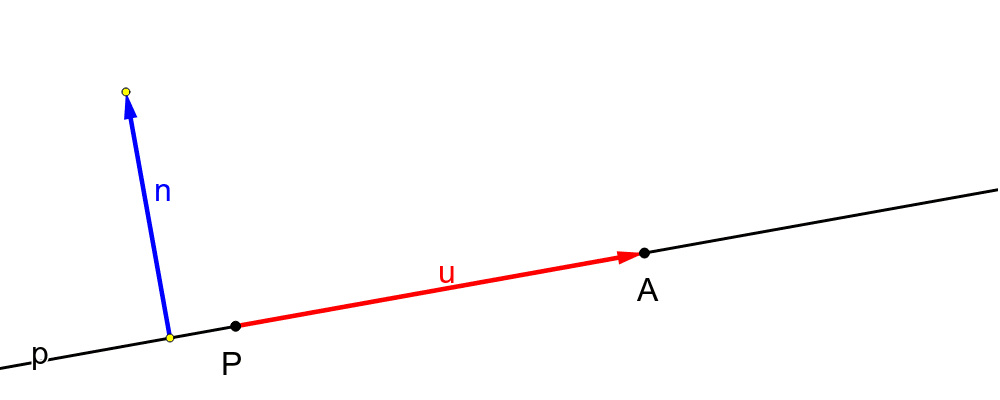
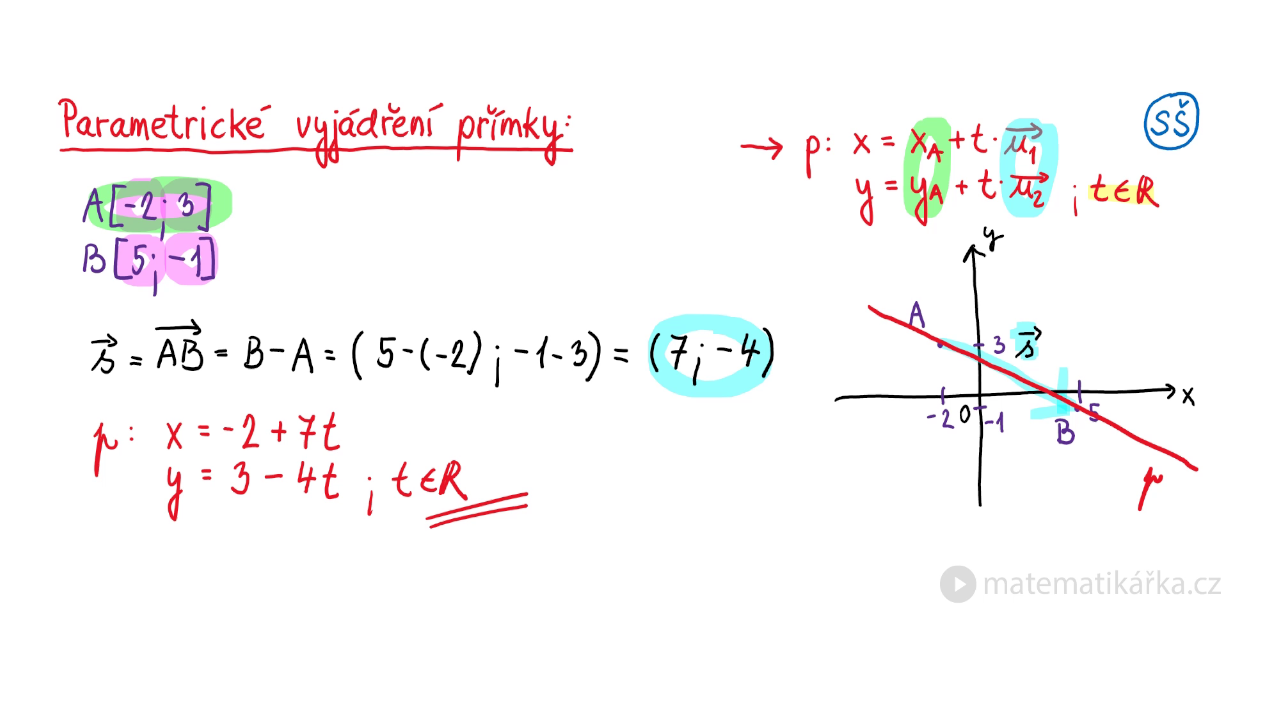
Každá přímka v rovině je určena dvěma různými body A a B. Tyto body určují také vektor. My tento vektor pojmenujeme a využijeme jej pro zavedení parametrického vyjádření přímky. Jestliže A, B jsou dva různé body, pak vektor u = B – A nazýváme směrový vektor přímky AB.Vektor n = (a, b) se nazývá normálový vektor přímky p a je kolmý ke směrovému vektoru u přímky p. Dvě přímky p, q jsou totožné právě tehdy, je-li obecná rovnice přímky p násobkem obecné rovnice přímky q. Dvě přímky p, q jsou rovnoběžné právě tehdy, je-li normálový vektor přímky p násobkem normálového vektoru přímky q.Parametrizace, parametrické vyjádření neboli parametrické rovnice geometrického útvaru (křivky, plochy) je zobrazení v matematice, které určuje souřadnice bodů tohoto útvaru jako funkce parametru. Opakem je implicitní rovnice útvaru například v podobě F(x,y) = 0.
Jak poznat že bod leží na přímce : Body A, B, C leží na jedné přímce, právě tehdy, když je vektor AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC.
Jak se sčítají vektory
Sčítáme-li dva vektory, tak prostě a jednoduše sečteme jejich x-ové složky a jejich y-ové složky. A tak dostaneme výsledný vektor.
Co to je jednotkový vektor : jednotkový vektor je vektor, který má velikost jedna. Budeme si tedy povídat o tom, jak z vektoru, který nemá velikost jedna udělat vektor, která je rovnoběžný a velikost jedna má. Celý kurz hezky seřazený najdete zde: http://www.mathematicator.com/search….
Délka vektoru se vypočte pomocí Pythagorovy věty. Pro normalizaci vektoru se vektor vydělí svojí délkou a získá se tak jednotkový (normalizovaný) vektor.
Normálový vektor n, je vektor kolmý na směrový vektor. Potřebujeme ho pro obecnou rovnici přímky (v rovině) a obecnou rovnici roviny (v prostoru). Souřadnice normálového vektoru n získáme například tak, že prohodíme souřadnice směrového vektrou, na který je kolmý, a u jedné souřadnice změníme znaménko.
Jak se počítá normálový vektor
Normálový vektor přímky dostaneme v rovině snadno prohozením souřadnic a jednoho znaménka →n=(3,1). Obecná rovnice má tedy tvar 3x+1y+c=0. Konstantu c určíme tak, aby přímka procházela zadanými body 3⋅3+1⋅2+c=0, odkud c=−11 a dostáváme hledanou rovnici přímky ve tvaru 3x+y−11=0.Jak určit body ležící na přímce je jednoduché – stačí zvolit jednu jeho souřadnici a z obecné rovnice dopočítat druhou. Zvolme si například hodnotu x-ové souřadnice jako 1. Dosadíme do obecné rovnice přímky a dopočítáme y-ovou souřadnici 2⋅1 – y + 3 = 0, y = 5.Bod – je základní geometrický pojem, bod obvykle označujeme křížkem a značíme jej velkým písmenem. Your browser does not support this audio format. Přímka – se zadává dvěma body, neboť každými dvěma body lze vést právě jednu přímku. Značíme ji dvěma body nebo častěji malým písmenem.
Přímka a rovina jsou k sobě kolmé právě tehdy, když je přímka kolmá ke všem přímkám roviny.
Co jsou to vektory : Vektor představuje ve fyzice a vektorovém počtu veličinu, která má kromě velikosti i směr. Tím se liší od obyčejného čísla, neboli skaláru, které má pouze velikost. Příkladem vektoru je síla — má velikost a směr, a více sil se skládá dohromady podle zákona o skládání sil – rovnoběžníkového pravidla.
Jak se zapisuji vektory : Velikost vektoru a směr vektoru je stejná jako velikost a směr orientované úsečky, která reprezentuje daný vektor. Vektory obyčejně zapisujeme tučně a s šipkou stejně jako orientovanou úsečku. Můžeme tak mít vektor nebo zkráceněji vektor . Jedna konkrétní orientovaná úsečka pak představuje umístění vektoru.
Jak vypočítat normu vektoru
Definice normy a úhlu vektorů
Vektor v se nazývá normovaný (jednotkový), je-li ‖v‖=1. Jinak řečeno, norma vektoru je odmocnina ze skalárního součinu tohoto vektoru samého se sebou. Nechť V je reálný vektorový prostor se skalárním součinem f. cosφ=f(u,v)‖u‖‖v‖,0≤φ≤π.
Už jsme si řekli, že jednotkový vektor má nějaký určitý směr, ale co je důležité, je to, že jeho velikost je rovna jedné.Při daném směrovém vektoru nám k získání vektoru normálového stačí prohodit souřadnice a u jedné z nich změnit znaménko.
Jak se pocita vzdalenost bodů od přímky : Vzdálenost bodu od přímky je rovna velikost „nejkratší“ úsečky vedené od tohoto bodu k dané přímce.