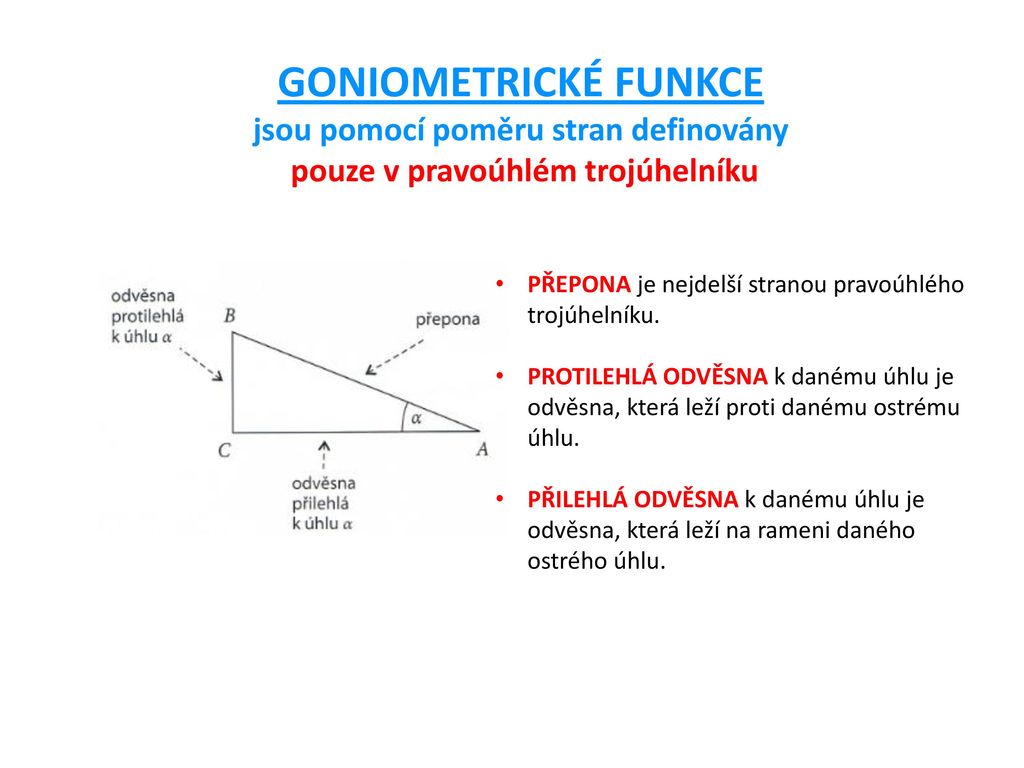
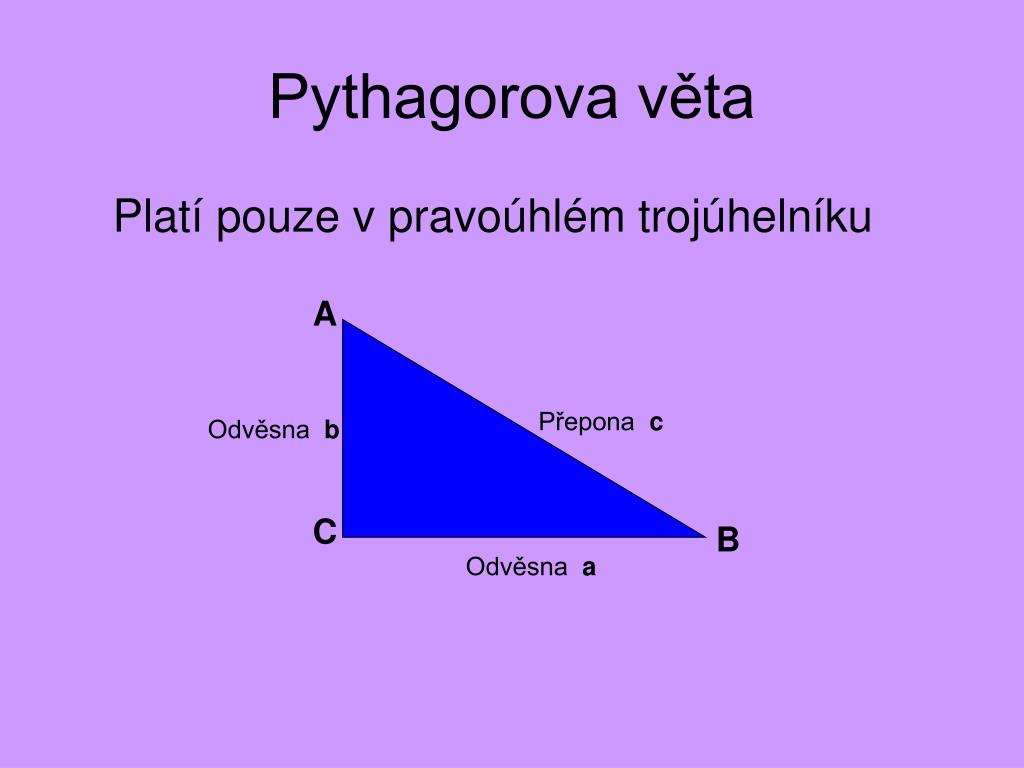
Pravoúhlý trojúhelník je takový trojúhelník, jehož jeden vnitřní úhel je pravý, tzn. má velikost 90°; jinými slovy, dvě ze stran pravoúhlého trojúhelníka jsou na sebe kolmé.Každý trojúhelník má tři výšky. Menší straně odpovídá větší výška. Přímky, na nichž leží výšky, se protínají v jednom bodě, který se nazývá ortocentrum nebo také výšiště. Ortocentrum leží uvnitř trojúhelníku, pokud je ostroúhlý.Jak zjistit (bez rýsování), jestli je trojúhelník pravoúhlý Jestliže v trojúhelníku platí, že součet druhých mocnin délek dvou kratších stran je roven druhé mocnině délky nejdelší strany, potom je tento trojúhelník pravoúhlý.
Jak mám vypočítat obsah pravoúhlého trojúhelníku : Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami. Pythagorovu větu můžeme zapsat vztahem c 2 = a 2 + b 2 c^2 = a^2 + b^2 c2=a2+b2, kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.
Co platí v pravoúhlém trojúhelníku
V každém pravoúhlém trojúhelníku platí , kde je délka přepony, , jsou délky jeho odvěsen. Jiná formulace věty. Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců nad jeho odvěsnami.
Co platí pro rovnoramenný trojúhelník : Kromě vlastností společných pro každý trojúhelník má rovnoramenný trojúhelník navíc tyto vlastnosti: Je osově souměrný podle osy procházející hlavním vrcholem a středem základny. Úhly při základně jsou shodné. Výšky příslušné ramenům jsou shodné.
Těžnice se protínají v jednom společném bodě, který označujeme T. Tento bod se nazývá těžiště a nachází se vždy uvnitř trojúhelníku. Těžiště rozděluje každou těžnici v poměru 2:1, kde větší část těžnice se nachází mezi vrcholem a těžištěm.
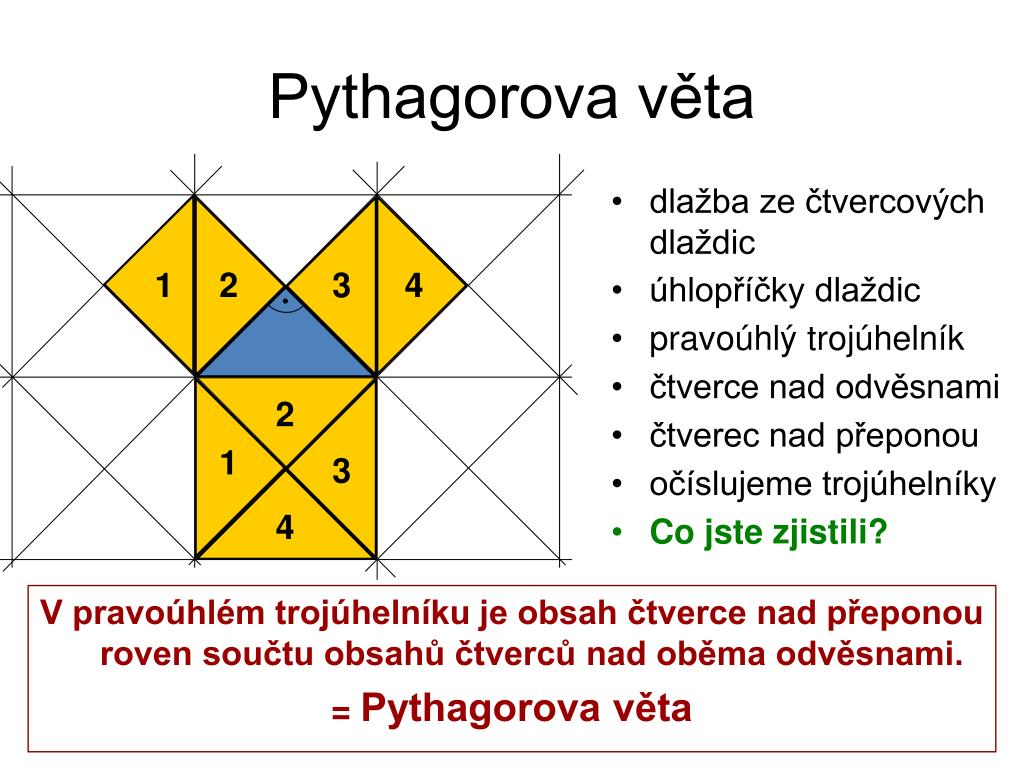
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Jak se počítá délka přepony
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .V rovnoramenném trojúhelníku jsou oba úhly u základny stejné. V pravoúhlém trojúhelníku je velikost jednoho úhlu 90°, součet velikostí zbývajících dvou úhlů je také 90°.X-ová souřadnice bodu, kde se koncové rameno úhlu protíná s jednotkovou kružnicí. Sinus θ se pak rovná y-ové souřadnici průsečíku koncového ramena s jednotkovou kružnicí. V podstatě pro jakýkoliv úhel platí, že je jeho sinus a kosinus určen bodem.
Rovnoramenný lichoběžník:
Ramena jsou shodné úsečky. Úhly při základně jsou shodné. Při delší základně jsou úhly ostré a při kratší základně jsou tupé. Rovnoramenný lichoběžník má jednu osu souměrnosti, která je společnou osou obou základen.
Co je to pátá výšky : Tímto pojmem ale můžeme chápat i celou přímku, na níž dotyčná úsečka leží. Například výška va na stranu a trojúhelníku ABC je úsečka spojující vrchol A s jeho kolmým průmětem Pa do přímky BC resp. přímka APa. Tyto průměty nazýváme paty výšek.
Co vime o trojúhelníku : Nejnápadnější pravidlo: Trojúhelník má tolik shodných úhlů, kolik má shodných stran. Navíc víme, kde shodné úhly leží. U rovnoramenného trojúhelníka jsou shodné strany a, b a shodné úhly α a β (úhly ležící proti shodným stranám) ⇒ proti shodným stranám leží shodné úhly.
Jak vypočítat stranu BV trojúhelníku
Vysvětlíme si, jak lze vypočítat délku strany trojúhelníku při zadaném obsahu a délce dvou dalších stran. Pro výpočet použijeme vzorec pro obsah trojúhelníku (strana krát výška)/2.
V pravoúhlém trojúhelníku platí, že velikost plochy čtverce nad odvěsnou je stejná jako plocha obdélníku (vztyčeného výškou) ve čtverci nad odvěsnou. Pythagorova věta: V každém pravoúhlém trojúhelníku je součet obsahů čtverců nad odvěsnami stejný jako obsah čtverce nad přeponou.Platí Pythagorova věta
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců sestrojených nad jeho odvěsnami. Délku přepony pravoúhlého trojúhelníku vypočteme podle vzorce c2 = a2 + b2.
Jak poznat rovnoramenný trojúhelník : Rovnoramenný trojúhelník je trojúhelník, který má (alespoň) dvě strany shodné.