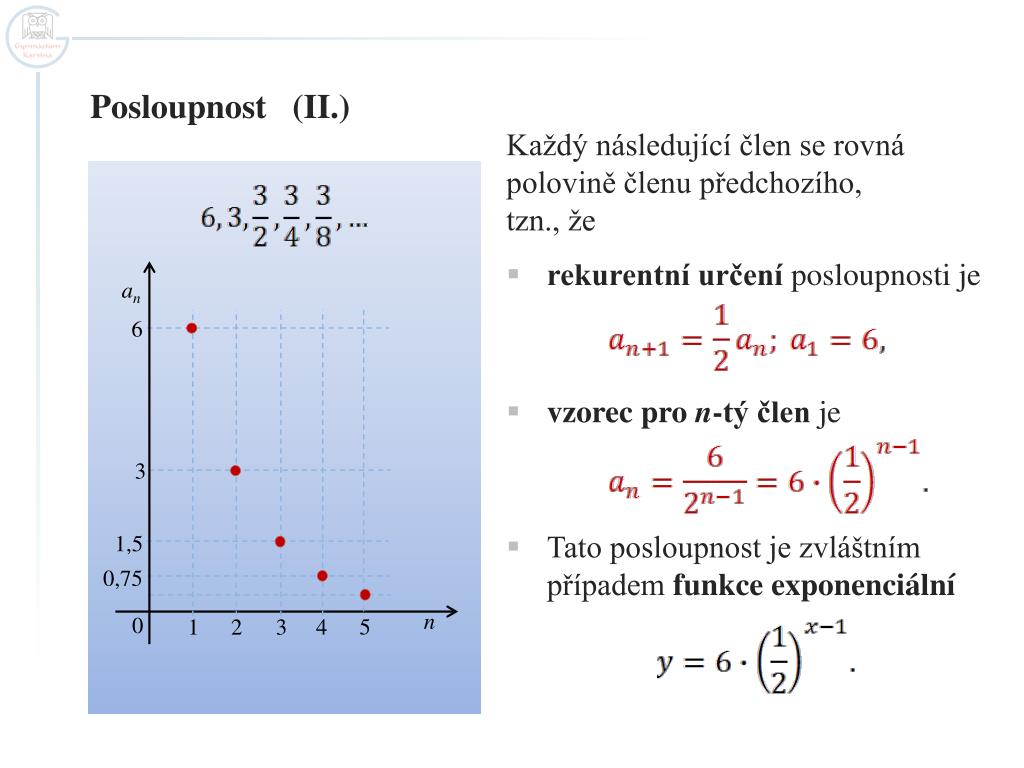
Rekurentní zadání posloupnosti
Tento zápis nám říká, že první člen posloupnosti se rovná dvěma a další členy získáme tak, že vynásobíme předchozí člen dvakrát a přičteme jedničku.Posloupnost je aritmetická, proto známe vzorec pro n-tý člen an=a1+(n−1)⋅d. Členy a2,a3 vyjádříme pomocí prvního členu a diference a dosadíme do rovnic ze zadání.Posloupnost (sekvence) je v matematice konečná nebo nekonečná sada objektů, v níž záleží na pořadí a objekty se mohou opakovat. Například zápis libovolného slova (nebo libovolný řetězec znaků) lze považovat za konečnou posloupnost písmen. Pokud je posloupnost konečná, často ji nazýváme uspořádanou n-ticí.
Jak se počítá posloupnost : Aritmetická posloupnost
a n = a 1 + ( n − 1 ) d . Takže pro příklad si vezmeme opět sudá čísla, kde je diference dva a první sudé číslo je také dvojka. Pak platí, druhé sudé číslo získáme tak, že k prvnímu přičteme dvojku. Pokud ještě jednou přičteme dvojku, získáme třetí sudé číslo.
Co je to rekurentní
Rekurentní infekce je opakovaná infekce určitým patogenem, obvykle virem. Na rozdíl od primoinfekce již tělo v tomto okamžiku protilátky vůči tomuto patogenu, proto je i imunitní reakce jiná. Rekurentní infekce se během života mohou opakovat (vracet) i vícekrát.
Co je to rekurentní vzorec : Rekurentní vzorec určuje člen posloupnosti pomocí znalosti jednoho nebo více předcházejících členů.
Limita posloupnosti je číslo, kterému se členy posloupnosti postupně přibližují, popřípadě jej dosahují, když se jejich pořadí blíží nekonečnu.
Posloupnost může být konečná i nekonečná. Členy posloupnosti typicky zapisujeme pomocí indexů: a n a_n an značí n-tý člen posloupnosti a. Posloupnosti můžeme zapsat různými způsoby: výčtem členů: a = ( 7 , 10 , 13 , 16 , 19 , 22 ) a = (7, 10, 13, 16, 19, 22) a=(7,10,13,16,19,22)
Kdy je posloupnost konvergentní
Posloupnost se nazývá konvergentní, pokud má vlastní (reálnou) limitu A. Posloupnost se nazývá divergentní, pokud není konvergentí. Každá posloupnost má nejvýše jednu limitu.Relaps / rekurence / recidiva jsou různá označení návratu onemocnění, které po předchozí léčbě nebylo prokazatelné.Posloupnost, jejíž limitou je reálné číslo , se nazývá konvergentní. (Říkáme také, že posloupnost konverguje k číslu .) Posloupnost, která nemá limitu nebo jejíž limita je rovna , se nazývá divergentní. Každá posloupnost může mít nejvýše jednu limitu.
Definice vlastní limity posloupnosti. Je na čase si limitu posloupnosti pořádně zadefinovat. Posloupnost { a n ∈ R } n = 1 ∞ má vlastní limitu a, (konverguje k limitě a ∈ ℝ, je konvergentní) jestliže ke každému ε > 0 existuje n0∈ℕ takové, že pro všechna n>n0 platí |an − a| < ε.
Kdy je řada konvergentní : Jelikož řada je definovaná jako součet, budeme se hlavně zajímat o to, zda danou řadu lze nebo nelze sečíst, a pokud ano, tak jaký je tento součet. Definice: Řada se nazývá konvergentní, pokud je její součet reálné číslo.
Co to je konvergentní : Konvergence (z lat. con-vergere, ohýbat k sobě) je pojem označující sbíhání, sbíhavost, sbližování, popř. vývoj, který vede ke sblížení. O daných vlastnostech, které se sbližují, říkáme, že konvergují.
Kdy je ráda konvergentní
Jelikož řada je definovaná jako součet, budeme se hlavně zajímat o to, zda danou řadu lze nebo nelze sečíst, a pokud ano, tak jaký je tento součet. Definice: Řada se nazývá konvergentní, pokud je její součet reálné číslo.
[Latina], řízení, řízenost – vyjádření větného vztahu determinace, kdy řídící člen větné dvojice (sloveso, adjektivum nebo substantivum) určuje pád závislého čtenu (vazba s akuzativem – chystat léčku).Konvergence (z lat. con-vergere, ohýbat k sobě) je pojem označující sbíhání, sbíhavost, sbližování, popř. vývoj, který vede ke sblížení. O daných vlastnostech, které se sbližují, říkáme, že konvergují.
Co je to konvergentní myšlení : Konvergentní myšlení se uplatňuje v úlohách s jedním správným řešením nebo v úlohách s konečným počtem správných řešení. Správná řešení vždy logicky vyplývají z daných informací v úloze. Je to tedy takové myšlení, při kterém se logicky a algoritmicky postupuje ke správnému závěru.